Narysuj wykres funkcji liniowej, podaj punkt przecięcia się wykresu z osią OY oraz monotoniczność:
a) \(y=x+1\)
b) \(y=\frac{1}{3}x-1\)
c) \(y=-2x+3\)
d) \(y=-\frac{1}{2}x-2\)
Do narysowania funkcji liniowej, potrzeba minimum 2 punktów, trzeba je wyliczyć podstawiając za \(x\) dowolną wartość i wyliczając \(y\). Aby określić monotoniczność, trzeba określić współczynnik kierunkowy (dla \(a>0\) rosnąca; dla \(a<0\) malejąca; dla \(a=0\) stała). Punkt przecięcia z osią OY wskazujemy przez współczynnik \((0;b)\).
Rozwiązanie
a)
\(y=x+1\)
Zadanie zaczynamy od tabeli, następnie narysowania wykresu funkcji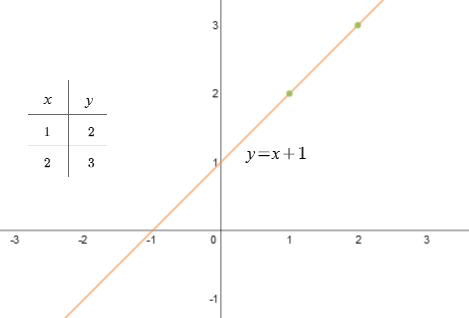
Podana funkcja przecina się z osią OY w punkcie \((0;1)\). Podana funkcja jest rosnąca.
b)
\(y=\frac{1}{3}x-1\)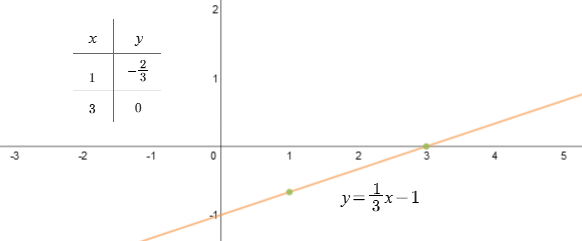
d)
\(y=-\frac{1}{2}x-2\)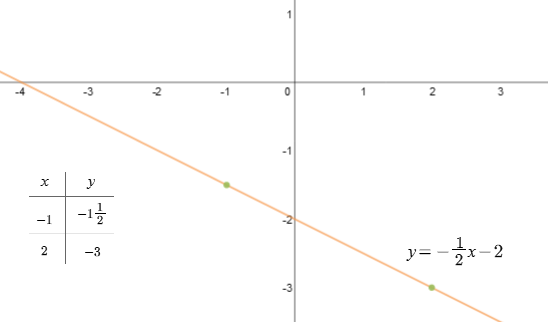
Funkcja przecina się z osią OY w punkcie \((0;-2)\). Podana funkcja jest malejąca, ponieważ \(a<0\) i wynosi \(-\frac{1}{2}\).
a) \(y=x+1\)
b) \(y=\frac{1}{3}x-1\)
c) \(y=-2x+3\)
d) \(y=-\frac{1}{2}x-2\)
Do narysowania funkcji liniowej, potrzeba minimum 2 punktów, trzeba je wyliczyć podstawiając za \(x\) dowolną wartość i wyliczając \(y\). Aby określić monotoniczność, trzeba określić współczynnik kierunkowy (dla \(a>0\) rosnąca; dla \(a<0\) malejąca; dla \(a=0\) stała). Punkt przecięcia z osią OY wskazujemy przez współczynnik \((0;b)\).
Rozwiązanie
a)
\(y=x+1\)
Zadanie zaczynamy od tabeli, następnie narysowania wykresu funkcji

Podana funkcja przecina się z osią OY w punkcie \((0;1)\). Podana funkcja jest rosnąca.
b)
\(y=\frac{1}{3}x-1\)
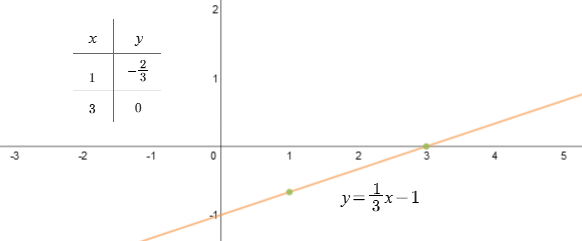
Funkcja przecina się z osią OY w punkcie \((0;-1)\). Podana funkcja jest rosnąca, ponieważ \(a>0\) i wynosi \(\frac{1}{3}\).
c)
\(y=-2x+3\)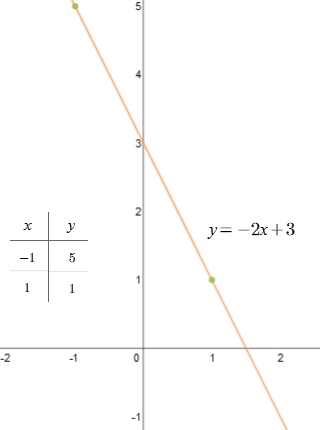
d)
\(y=-\frac{1}{2}x-2\)

Funkcja przecina się z osią OY w punkcie \((0;-2)\). Podana funkcja jest malejąca, ponieważ \(a<0\) i wynosi \(-\frac{1}{2}\).
Jak obliczyć funkcja liniowa – zadanie 2 - wyniki