Wykres funkcji logarytmicznej - opis

Wszystkie funkcje logarytmiczne \(y=\log_{a} x\), można podzielić na dwie grupy w zależności od parametru \(a\) (podstawy logarytmu).

Dla \(a\) większego od \(1\)


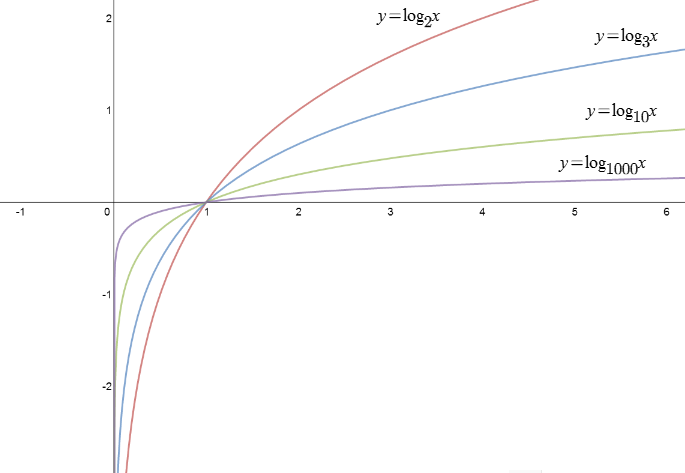
Oraz dla \(a\) mniejszego od \(1\) i oczywiście większego od \(0\).


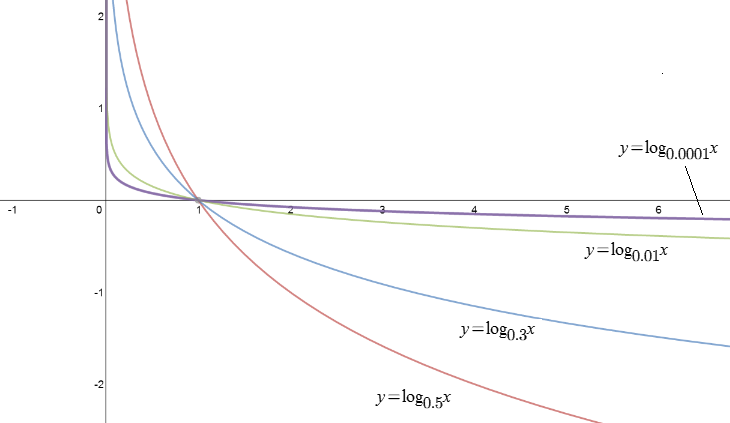
Własności funkcji logarytmicznej \(f(x)=\log_{a}x\)

- Dziedzina - \(D=(0;+\infty)\) lub \(D=\mathbb{R_{+}}\)
- Zbiór wartości - \(ZW=(-\infty;+\infty)\) lub \(ZW= \mathbb{R}\)
- Miejsce zerowe - \(x=1\)
- monotoniczność
- dla \(a>0\) funkcja jest rosnąca,
- dla \(a\:\epsilon \:(0;1)\) funkcja jest malejąca,
- funkcja logarytmiczna jest różnowartościowa
- funkcja \(f(x)=\log_{a}x\) jest styczna do osi OX


Przykładowe zadania

Zad. 1) Narysuj wykres funkcji:

a) \(y=\log_{2}x\)

b) \(y=\log_{5}x\)

c) \(y=\log_{\frac{1}{4}}x\)

d) \(y=\log_{\frac{2}{5}}x\)      Zobacz rozwiązanie