Aby obliczyć punkty przegięcia (definicja) trzeba:
1) obliczyć drugą pochodną funkcji,
2) przyrównać ją do zera,
3) rozwiązać równanie, (sprawdzić czy należy do dziedziny funkcji)
4) sprawdzić znak drugiej pochodnej po lewej i prawej stronie argumentu x jaki wyjdzie nam z równania.
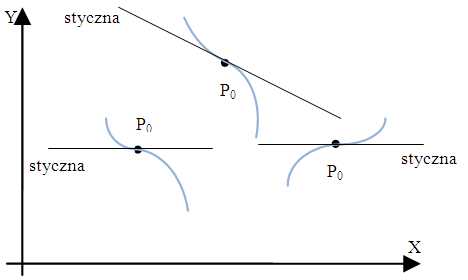
Zagadnienie to jest ściśle związana z pojęciem wklęsłości i wypukłości funkcji (definicją, przykład).
Jak to zrobić najlepiej zaprezentuje przykład:
Przykład 1
Wyznacz punkty przegięcia funkcji \(f(x)=x^6\).
Pierwszą rzeczą jaką zawsze trzeba wykonać to wyznaczenie dziedziny funkcji, w tym przypadku to \(D_f=R\), czyli wszystkie liczby rzeczywiste, następnie trzeba obliczyć drugą pochodną (najpierw pierwszą pochodną, następnie z pierwszej pochodnej obliczamy pochodną, co daje nam drugą pochodną):
\(f(x)=x^6\)
\(f'(x)= 6x^5\)
\(f''(x)=(f'(x))'=30x^4\)
teraz przyrównujemy drugą pochodną do zera:
\(30x^4=0\)
i rozwiązujemy równanie
\(30x^4=0\:\:/ :30\)
\(x^4=0\)
\(x=0\)
mamy x=0, który jest podejrzany o bycie punktem przegięcia, następnie trzeba sprawdzić znak drugiej pochodnej po lewej i prawej stronie funkcji:
aby sprawdzić znak funkcji z lewej strony x=0 do drugiej pochodnej wstawimy np. -2
\(f''(-2)= (-2)^4= 16\)
wynikiem jest dodatnia liczba więc znak drugiej pochodnej z lewej strony x=0 jest \(+\)dodatni, następnie sprawdzimy znak z prawej strony x=0, podstawiając np. +3:
\(f(3)=3^4= 81\)
wynikiem jest liczba dodatnia więc znak drugiej pochodnej z lewej strony x=0 jest \(+\) dodatni. Z obu stron x=0 druga pochodna funkcji ma dodatni znak, oznacza to, że dla argumentu x=0 funkcja f(x) nie ma punktu przegięcia, gdyby z dwóch stron były różne znaki to byłby punkt przegięcia.
Przykład 2
Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji \(f(x)=e^{-x^2}\).
Dziedzina funkcji to \(D_f=R\).
Najpierw obliczamy drugą pochodną funkcji:
\(f'(x)=-2x\cdot e^{-x^2}\)
\(f''(x)= -2e^{-x^2}-2x(-2x)e^-{x^2}\)
\(f''(x)= -2e^{-x^2}+4x^2e^{-x^2}\) lub \(f''(x)= 2e^{-x^2}(2x^2-1)\)
następnie wyliczoną pochodną przyrównujemy do zera i rozwiązujemy.
\(f''(x)=0\)
\(2e^{-x^2}(2x^2-1)=0\)
\(2e^{-x^2}=0 \:\:\:\vee\:\:\:2x^2-1=0\)
\(2x^2=1\)
\(x^2=\dfrac{1}{2}\)
\(x_1= \dfrac{\sqrt{2}}{2}\:\:\:\vee\:\:\:x_2=-\dfrac{\sqrt{2}}{2}\)
mamy więc dwa punkty podejrzane o bycie punktem przegięcia, teraz trzeba sprawdzić znak drugiej pochodnej w każdym z trzech przedziałów (wyznaczonych przez \(x_1\) oraz \(x_2\)), czyli
1 - \((-\infty;-\dfrac{\sqrt{2}}{2})\)
2 - \((-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2})\)
3 - \((\dfrac{\sqrt{2}}{2};+\infty)\)
więc:
1 - dla \((-\infty;-\dfrac{\sqrt{2}}{2})\) wybierzemy -10 i wstawimy do wzoru drugiej pochodnej,
\(f''(-10)= 2e^{-(-10)^2}(2(-10)^2-1)=2e^{-100}\cdot 199=398e^{-100}\)
wynik jest liczbą dodatnią, co oznacza, że funkcja jest wypukłą.
2 - dla \((-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2})\) wybierzemy \(0\) bo należy do przedziału,
\(f''(0)= 2e^{-(0)^2}(2(0)^2-1)=2e^0\cdot (-1)=-2\)
wynik jest liczbą ujemną, co oznacza, że funkcja podstawowa w tym przedziale jest wklęsła.
3 - dla \((\dfrac{\sqrt{2}}{2};+\infty)\) wybierzemy liczbę 10,
\(f''(10)= 2e^{-(10)^2}(2(10)^2-1)=2e^{-100}\cdot 199=398e^{-100}\)
wynik podobnie jak w pierwszym przedziale jest liczbą dodatnią, co oznacza, że funkcja w tym przedziale jest wypukła.
Możemy juz jednoznacznie określić punkty przegięcia:
dla \(x= -\dfrac{\sqrt{2}}{2}\) z lewej strony druga pochodna jest dodatnia, z prawej jest ujemna - wniosek funkcja posiada punkt przegięcia dla \(x= -\dfrac{\sqrt{2}}{2}\)
dla \(x= \dfrac{\sqrt{2}}{2}\) z lewej strony druga pochodna jest ujemna, z prawej jest dodatnia - wniosek funkcja posiada punkt przegięcia dla \(x= \dfrac{\sqrt{2}}{2}\)
pozostaje wyliczyć jedynie współrzędne punktów przegięcia
\(f(\dfrac{\sqrt{2}}{2})=e^{-\left ( \frac{\sqrt{2}}{2} \right )^2}=e^{-\frac{1}{2}}\)
\(f(-\dfrac{\sqrt{2}}{2})=e^{-\left ( -\frac{\sqrt{2}}{2} \right )^2}=e^{-\frac{1}{2}}\)
Odpowiedź:
Funkcja posiada dwa punkty przegięcia \(A=\left ( -\frac{\sqrt{2}}{2};e^{-\frac{1}{2}} \right )\) oraz \(B=\left ( \frac{\sqrt{2}}{2};e^{-\frac{1}{2}} \right )\), funkcja jest wklęsła dla \(x\:\epsilon \:(-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2})\), funkcja jest wypukła dla \(x\:\epsilon \:(-\infty;-\dfrac{\sqrt{2}}{2})\:\cup\:(\dfrac{\sqrt{2}}{2};+\infty)\)
aby sprawdzić znak funkcji z lewej strony x=0 do drugiej pochodnej wstawimy np. -2
\(f''(-2)= (-2)^4= 16\)
wynikiem jest dodatnia liczba więc znak drugiej pochodnej z lewej strony x=0 jest \(+\)dodatni, następnie sprawdzimy znak z prawej strony x=0, podstawiając np. +3:
\(f(3)=3^4= 81\)
wynikiem jest liczba dodatnia więc znak drugiej pochodnej z lewej strony x=0 jest \(+\) dodatni. Z obu stron x=0 druga pochodna funkcji ma dodatni znak, oznacza to, że dla argumentu x=0 funkcja f(x) nie ma punktu przegięcia, gdyby z dwóch stron były różne znaki to byłby punkt przegięcia.
Przykład 2
Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji \(f(x)=e^{-x^2}\).
Dziedzina funkcji to \(D_f=R\).
Najpierw obliczamy drugą pochodną funkcji:
\(f'(x)=-2x\cdot e^{-x^2}\)
\(f''(x)= -2e^{-x^2}-2x(-2x)e^-{x^2}\)
\(f''(x)= -2e^{-x^2}+4x^2e^{-x^2}\) lub \(f''(x)= 2e^{-x^2}(2x^2-1)\)
następnie wyliczoną pochodną przyrównujemy do zera i rozwiązujemy.
\(f''(x)=0\)
\(2e^{-x^2}(2x^2-1)=0\)
\(2e^{-x^2}=0 \:\:\:\vee\:\:\:2x^2-1=0\)
\(2x^2=1\)
\(x^2=\dfrac{1}{2}\)
\(x_1= \dfrac{\sqrt{2}}{2}\:\:\:\vee\:\:\:x_2=-\dfrac{\sqrt{2}}{2}\)
mamy więc dwa punkty podejrzane o bycie punktem przegięcia, teraz trzeba sprawdzić znak drugiej pochodnej w każdym z trzech przedziałów (wyznaczonych przez \(x_1\) oraz \(x_2\)), czyli
1 - \((-\infty;-\dfrac{\sqrt{2}}{2})\)
2 - \((-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2})\)
3 - \((\dfrac{\sqrt{2}}{2};+\infty)\)
więc:
1 - dla \((-\infty;-\dfrac{\sqrt{2}}{2})\) wybierzemy -10 i wstawimy do wzoru drugiej pochodnej,
\(f''(-10)= 2e^{-(-10)^2}(2(-10)^2-1)=2e^{-100}\cdot 199=398e^{-100}\)
wynik jest liczbą dodatnią, co oznacza, że funkcja jest wypukłą.
2 - dla \((-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2})\) wybierzemy \(0\) bo należy do przedziału,
\(f''(0)= 2e^{-(0)^2}(2(0)^2-1)=2e^0\cdot (-1)=-2\)
wynik jest liczbą ujemną, co oznacza, że funkcja podstawowa w tym przedziale jest wklęsła.
3 - dla \((\dfrac{\sqrt{2}}{2};+\infty)\) wybierzemy liczbę 10,
\(f''(10)= 2e^{-(10)^2}(2(10)^2-1)=2e^{-100}\cdot 199=398e^{-100}\)
wynik podobnie jak w pierwszym przedziale jest liczbą dodatnią, co oznacza, że funkcja w tym przedziale jest wypukła.
Możemy juz jednoznacznie określić punkty przegięcia:
dla \(x= -\dfrac{\sqrt{2}}{2}\) z lewej strony druga pochodna jest dodatnia, z prawej jest ujemna - wniosek funkcja posiada punkt przegięcia dla \(x= -\dfrac{\sqrt{2}}{2}\)
dla \(x= \dfrac{\sqrt{2}}{2}\) z lewej strony druga pochodna jest ujemna, z prawej jest dodatnia - wniosek funkcja posiada punkt przegięcia dla \(x= \dfrac{\sqrt{2}}{2}\)
pozostaje wyliczyć jedynie współrzędne punktów przegięcia
\(f(\dfrac{\sqrt{2}}{2})=e^{-\left ( \frac{\sqrt{2}}{2} \right )^2}=e^{-\frac{1}{2}}\)
\(f(-\dfrac{\sqrt{2}}{2})=e^{-\left ( -\frac{\sqrt{2}}{2} \right )^2}=e^{-\frac{1}{2}}\)
Odpowiedź:
Funkcja posiada dwa punkty przegięcia \(A=\left ( -\frac{\sqrt{2}}{2};e^{-\frac{1}{2}} \right )\) oraz \(B=\left ( \frac{\sqrt{2}}{2};e^{-\frac{1}{2}} \right )\), funkcja jest wklęsła dla \(x\:\epsilon \:(-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2})\), funkcja jest wypukła dla \(x\:\epsilon \:(-\infty;-\dfrac{\sqrt{2}}{2})\:\cup\:(\dfrac{\sqrt{2}}{2};+\infty)\)
Punkt przegięcia Wasze opinie
zrozumiałam. zadania przejrzyście wyjaśnione. Bardzo dziekuję
Wszystko wytłumaczone, okuratnie, rzetelnie i sprawiedliwie.