Pierwiastkowanie to działanie odwrotne do potęgowania. Wynikiem pierwiastkowania, jak i liczba podpierwiastkowa, jest zawsze liczbą dodatnią.
Jak wygląda pierwiastek?
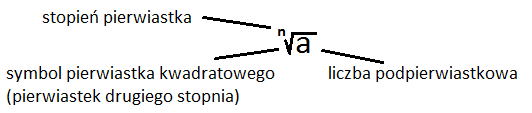
Pierwiastek kwadratowy z liczby nieujemnej x jest to taka liczba nieujemna y, która podniesiona do potęgi drugiej daje liczbę podpierwiastkową x.
\( { \sqrt{x} } =y \) bo y2 = x
Podstawowe działania na pierwiastkach
- mnożenie pierwiastków tego samego stopnia
\(\sqrt[n]{a}*\sqrt[n]{b}=\sqrt[n]{a*b}\) np. \(\sqrt[3]{8}*\sqrt[3]{27}=\sqrt[3]{8*27}=6\)
- podnoszenie pierwiastka do potęgi
\((\sqrt[n]{a})^m=\sqrt[n]{a^m}\) np. \((\sqrt[2]{3})^2=\sqrt[2]{3^2}=3\)
- wyłączanie czynnika przed znak pierwiastka
\(a\sqrt[n]{b}=\sqrt[n]{a^nb}\) np. \(2\sqrt[3]{4}=\sqrt[3]{2^34}=\sqrt[3]{32}\)
- dzielenie pierwiastków
\({\frac{\sqrt[n]{a}}{\sqrt[n]{b}}}=\sqrt[n]{\frac{a}{b}}\) np. \({\frac{\sqrt[3]{5}}{\sqrt[n]{8}}}=\sqrt[3]{\frac{5}{8}}\)
Pierwiastki Wasze opinie