Pojęcie pochodnej jest fundamentem rachunku nowoczesnej matematyki i fizyki. Fizycznie pochodna przedstawia szybkość zachodzących zmian, geometrycznie pochodna wyznacza styczną do funkcji w danym punkcie.
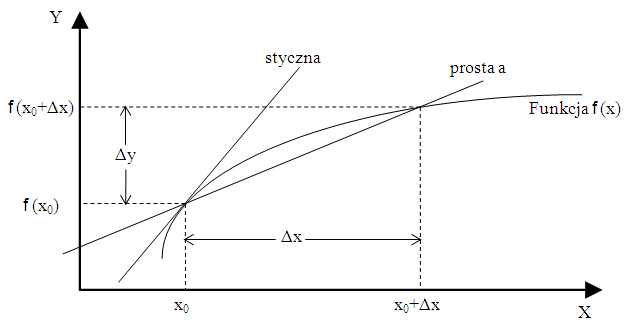
Im mniejsze \(\Delta x\) tym prosta \(a\) jest bliższa stycznej.
Fizyczny sposób wyobrażenia pochodnej
Wyobraźmy sobie, że na wykresie powyżej na osi \(X\) mamy czas \((t)\) a na osi \(Y\) mamy drogę \((S)\) lub prędkość \((V)\), wtedy pochodną możemy opisać jako \(V=\frac{\Delta S}{\Delta t}\) lub \(a=\frac{\Delta V}{\Delta t}\), czyli prędkość \((V)\) jest pochodną drogi \((S)\) po czasie \((t)\), lub przyspieszenie \((a)\) jest pochodną prędkości \((V)\) po czasie \((t)\). Pochodna oznacza szybkość zmian, tzn. jeśli ciało (samochód) porusza się ze stałą prędkością \((V)\) to pochodna po czasie \((t)\) (czyli przyspieszenie \((a)\)) będzie równe zero, lub jeśli przebyta droga \((S)\) się nie zmienia to pochodna wyniesie zero (prędkość \((V)\)) - dlatego pochodna z liczby to zero. Jeśli samochód zwiększa swoją prędkość jednostajnie \((V)\) to pochodna (przyspieszenie \((a)\)) będzie wartością stałą, jeśli samochód oddala się jednostajnie \((S)\) to pochodna (prędkość \((V)\)) będzie wartością stałą, czyli będzie jechał ze stałą prędkością - dlatego pochodna z funkcji liniowej to liczba (stała).
Wzór obliczania pochodnej funkcji z definicji nie jest łatwy w używaniu. Znacznie szybciej i prościej oblicza się pochodną z gotowych wzorów lub schematów. Obliczanie pochodnej z definicji zostawmy matematykom teoretykom. Obliczmy dla przykładu pochodną funkcji z definicji jednak nie polecam stosować tego toku postępowania:
Przykład 1:
Oblicz pochodną funkcji \(f(x)=x^3\) w punkcie \(x_0=2\):
\(f'(2)= \lim\limits_{\Delta x \to 0} \dfrac{f(2 + \Delta x) - f(2)}{\Delta x}=
\lim\limits_{\Delta x \to 0} \dfrac{(2 + \Delta x)^3 - 2^3}{\Delta x}= \)
\(\lim\limits_{\Delta x \to 0} \dfrac{2^3+3\cdot 2^2\cdot \Delta x +3\cdot 2 \cdot (\Delta x)^2- 2^3}{\Delta x}= \)
\(\lim\limits_{\Delta x \to 0} \dfrac{12\cdot \Delta x +6 \cdot (\Delta x)^2}{\Delta x}=
\lim\limits_{\Delta x \to 0} \dfrac{\Delta x\cdot (12 +6 \cdot \Delta x)}{\Delta x}= \)
\(\lim\limits_{\Delta x \to 0} 12 +6 \cdot \Delta x=
\lim\limits_{\Delta x \to 0} 12 +6 \cdot \Delta x=12\)
Wartość pochodnej funkcji w punkcie \(x=2\) wynosi \(f'(2)=12\)
Przykład 2:
Oblicz ogólny wzór pochodnej funkcji \(f(x)= x^2\):
\(f'(x)= \lim\limits_{\Delta x \to 0} \dfrac{f(x + \Delta x) - f(x)}{\Delta x}=
\lim\limits_{\Delta x \to 0} \dfrac{(x + \Delta x)^2 - x^2}{\Delta x}= \)
\(=\lim\limits_{\Delta x \to 0} \dfrac{x^2+2\cdot x\cdot \Delta x +(\Delta x)^2- x^2}{\Delta x}=
\lim\limits_{\Delta x \to 0} \dfrac{2\cdot x \cdot \Delta x + (\Delta x)^2}{\Delta x}= \)
\(\lim\limits_{\Delta x \to 0} \dfrac{\Delta x\cdot (2\cdot x + \Delta x)}{\Delta x}=
\lim\limits_{\Delta x \to 0} 2 \cdot x + \Delta x=2\cdot x \)
pochodna funkcji wynosi \(f(x)=2\cdot x\)
W życiu codziennym nie stosuje się takiego sposobu obliczania pochodnej. Aby obliczyć pochodną trzeba znać cztery zasady obliczania pochodnych oraz kilka podstawowych wzorów obliczania funkcji, w tablicach zamieszczone są wzory pochodnych najczęściej obliczanych pochodnych.
Cztery zasady obliczania pochodnych
1) \((f(x)+g(x))'=f'(x)+g'(x)\)
\((f(x)-g(x))'=f'(x)-g'(x)\)
2) \((f(x)\cdot g(x))'=f'(x)\cdot g(x)+f(x)\cdot g'(x)\)
3) \(\left ( \dfrac{f(x)}{g(x)} \right )'=\dfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{(g(x))^2}\)
4) \(\left ( f(g(x))\right )'=f'(g(x))\cdot g'(x)\)
Zasada pierwsza
Pochodna sumy (różnicy) funkcji jest sumą (różnicą) pochodnych tych funkcji. Oznacza to, że jeśli mamy funkcję złożoną z kilku członów dodawanych do siebie lub odejmowanych to pochodne takie liczymy oddzielnie.
\((f(x) \pm g(x))'=f'(x) \pm g'(x)\)
Przykład:
Oblicz pochodną z \(f(x)=x^2-sin(x)+\ln{x}\):
aby obliczyć pochodną z takiej funkcji najpierw podzielimy pochodną na trzy mniejsze funkcje:
\(f(x)=k(x)-g(x)+w(x)\)
\(f'(x)=[k(x)-g(x)+w(x)]'=k'(x)-g'(x)+w'(x)\)
gdzie:
\(k(x)=x^2\) ; \(k'(x)= 2x\)
\(g(x)=sin(x)\) ; \(g'(x)=cos(x)\)
\(w(x)= \ln{x}\) ; \(w'(x)=\dfrac{1}{x}\)
tak więc:
\(f'(x)=2x-cos(x)+\dfrac{1}{x}\)
Zasada druga
Pochodną iloczynu nie możemy obliczyć tak jak pochodną sumy czy różnicy, tu sytuacja się trochę utrudnia, jednak wzór jest dość jasny, Jeśli mamy mnożenie dwóch funkcji to najpierw obliczamy pochodną pierwszej funkcji i mnożymy przez drugą, potem obliczamy pochodną drugiej funkcji i mnożymy przez pierwszą na końcu dodajemy do siebie te dwa człony.
Przykład:
Oblicz pochodną funkcji \(x^3\cdot \ln{x}\)
możemy sobie zapisać:
\(f(x)=x^3\) ; \(f'(x)=3x^2\)
\(g(x)=\ln{x}\) ; \(g'(x)=\dfrac{1}{x}\)
więc, podstawiamy do wzoru:
\(\left ( x^3\cdot \ln{x} \right )'=3x^2\ln{x}+x^3\cdot \dfrac{1}{x}\)
Zasada trzecia
\(\left ( \dfrac{f(x)}{g(x)} \right )'=\dfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{(g(x))^2}\)
Przykład:
Oblicz pochodną funkcji \(h(x)=\dfrac{x^4}{\sin x}\)
po podstawieniu:
\(f(x)= x^4\) ; \(f'(x)=4x^3\)
\(g(x)= \sin x\) ; \(g'(x)= \cos x\)
wstawiamy do wzoru:
\(\left ( \dfrac{x^4}{\sin x} \right )'=\dfrac{4x^3\cdot \sin x-x^4\cdot \cos x}{\sin x}\)
pochodna obliczona, teraz można ewentualnie uprościć wyrażenie, jednak to zostawimy dla chętnych.
Zasada czwarta
\(\left ( f(g(x))\right )'=f'(g(x))\cdot g'(x)\)
O pochodnej złożonej mówimy gdy mamy funkcję w której jest inna funkcja np. dla:
\({\color{DarkBlue} {\ln}} {\color{DarkGreen} {(\sin x)}}\) funkcją zewnętrzną jest \(\ln ()\), funkcją wewnętrzną jest \(\sin x\)
\({\color{DarkBlue} {\sqrt{{\color{DarkGreen} {tg(x)}}}}}\) funkcją zewnętrzną jest \(\sqrt{()}\), funkcją wewnętrzną jest \(tg(x)\)
\({\color{DarkBlue} {(x^2+3x)}}{\color{DarkGreen} {^5}}\) funkcją zewnętrzną jest \(( \:)^5\), funkcją wewnętrzną jest \(x^2+3x\)
aby rozwiązać podane przykłady wystarczy podstawić do wzoru tak, że funkcja zewnętrzna to \(f\) a funkcja wewnętrzna to \(g\).
podane przykłady należy rozwiązywać w następujący sposób:
\((\ln \sin x)'=\frac{1}{\sin x}\cdot \cos x\)
\((\sqrt{tg(x)})'=\dfrac{1}{2\sqrt{tg(x)}}\cdot \dfrac{1}{\cos^2x}\)
\(\left ( (x^2+3x)^5 \right )'=5\cdot(x^2+3)^4\cdot (2x+3)\)
Pochodna Wasze opinie