Kąt wpisany jest kątem wypukłym, którego wierzchołkiem jest dowolny punkt okręgu, natomiast ramiona są półprostymi, które zawierają cięciwy tego koła. Miary dowolnych dwóch kątów wpisanych w koło, opartych na tych samych łukach są równe. Jeżeli chodzi o dowolny kąt wpisany, oparty na półokręgu, to jest to kąt prosty (ma miarę \(90^o\)).
Kąt środkowy jest kątem, którego wierzchołek znajduje się w środku koła a ramionami są półproste zawierające promienie koła. Kąt ten może przyjmować wartość z przedziału \((0^o, 360^o)\). Można powiedzieć, że miara kąta środkowego jest częścią kąta pełnego, równego części okręgu, jakiej równy jest łuk, na którym ten kąt jest oparty.
Kąt wpisany oraz kąt środkowy są pojęciami blisko ze sobą związanymi.
Twierdzenie o kącie środkowym oraz kącie wpisanym opartym na tym samym łuku
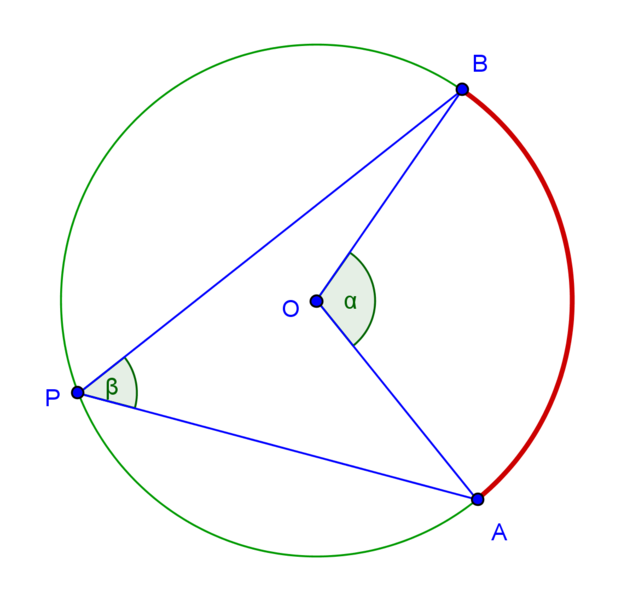
Miara kąta wpisanego jest dwa razy mniejsza od miary kąta środkowego opartego na tym samym łuku, tj. \({2 \alpha = \beta}\)
Kąt środkowy i wpisany Wasze opinie