Funkcje cyklometryczne - opis

Funkcje cyklometryczne (inaczej zwane funkcjami kołowymi) to funkcje odwrotne do funkcji trygonometrycznych ograniczonych do pewnych przedziałów.

Wiadomo, że funkcje trygonometryczne rozpatrujemy na całym zbiorze \({\mathbb{R}}\) oraz, że nie są to funkcje różnowartościowe. Sytuacja ulega zmianie, gdy zawęzimy ich dziedziny do pewnych przedziałów, tj.

\(sin :{\quad <- {\pi \over 2}, {\pi \over 2}> \quad \rightarrow \quad <-1,1>}\)

\(cos: {\quad <0, \pi> \quad \rightarrow \quad <-1,1>}\)

\(tg: {\quad (-{\pi \over 2}, {\pi \over 2}) \quad \rightarrow \quad \mathbb{R}}\)

\(ctg: {\quad (0, \pi) \quad \rightarrow \quad \mathbb{R}}\)

W ten sposób określone funkcje będą różnowartościowe oraz będą posiadały funkcje odwrotne. Przejdźmy zatem do krótkiego omówienia konkretnych funkcji.

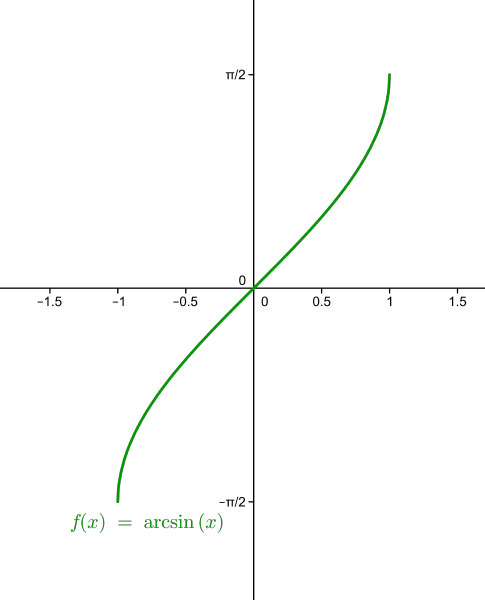
• Funkcją odwrotną do funkcji sin (sinus) obciętej do przedziału \({<-{\pi \over 2}, {\pi \over 2}>}\) nazywamy funkcję arc sin (arkus sinus). Dziedziną funkcji arc sin jest przedział \(<-1, 1>\), natomiast jej zbiorem wartości jest przedział \({ < -{\pi \over 2}, {\pi \over 2}>}\). Wykres funkcji arc sin powstaje przez odbicie symetryczne względem prostej \(y=x\) wykresu zawężonej funkcji sin.

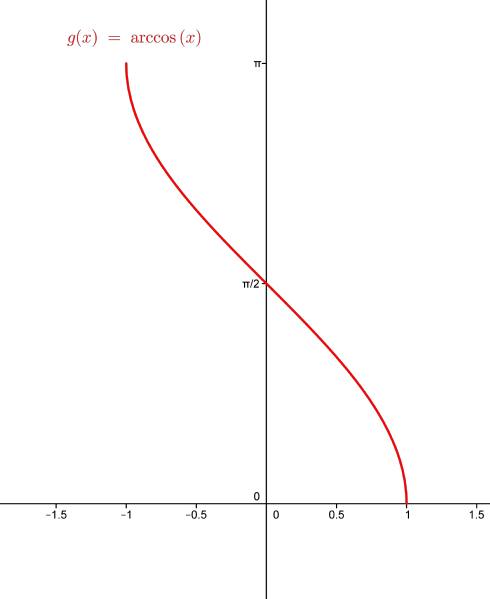
• Funkcją odwrotną do funkcji cos (cosinus) obciętej do przedziału \({<0,\pi >}\) nazywamy funkcję arc cos (arkus cosinus). Dziedziną funkcji arc cos jest przedział \(<-1, 1>\), natomiast zbiorem wartości tej funkcji jest przedział \({<0,\pi >}\). Wykres funkcji arc cos powstaje przez odbicie symetryczne względem prostej \(y=x\) wykresu zawężonej funkcji cos.

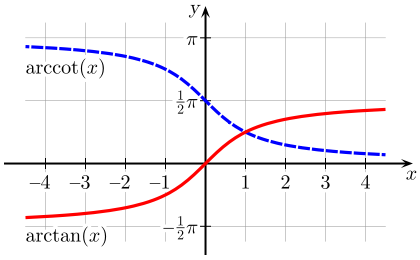
• Funkcją odwrotną do funkcji tg (tangens) obciętej do przedziału \({(-{\pi \over 2}, {\pi \over 2})}\) nazywamy funkcję arc tg (arkus tangens). Dziedziną funkcji arc tg jest \({\mathbb{R}}\), natomiast jej zbiorem wartości jest przedział \({(-{\pi \over 2}, {\pi \over 2})}\). Wykres funkcji arc tg powstaje przez odbicie symetryczne względem prostej \(y=x\) wykresu zawężonej funkcji tg.
• Funkcją odwrotną do funkcji ctg (cotangens) obciętej do przedziału \({(0,\pi )}\) nazywamy funkcję arc ctg (arkus cotangens). Dziedziną funkcji arc ctg jest \({\mathbb{R}}\), natomiast jej zbiorem wartości jest przedział \({(0,\pi )}\). Wykres funkcji arc ctg powstaje przez odbicie symetryczne względem prostej \(y=x\) wykresu zawężonej funkcji ctg.

Własności funkcji cyklometrycznych wynikają głównie z twierdzeń o funkcjach odwrotnych. Wszystkie te funkcje są ciągłe oraz różniczkowalne, ponadto:

arc sin - funkcja rosnąca,

arc cos - funkcja malejąca,

arc tg - funkcja rosnąca,

arc ctg - funkcja malejąca.

Podstawowe tożsamości funkcji cyklometrycznych:

\(arc sin x + arc cos x = {\pi \over 2} \) dla każdego \({x \in <-1, 1>}\)

\(arc tg x + arcctgx= {\pi \over 2}\) dla każdego \(x {\in \mathbb{R}}\)