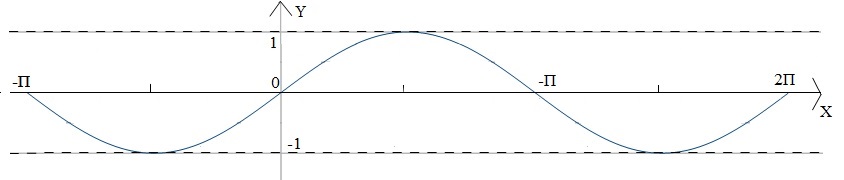
Własności funkcji \(y = \text{sin} \: x\):
• Dziedziną tej funkcji jest zbiór liczb rzeczywistych
\(y \in <-1, 1>\)
• Funkcja jest okresowa o okresie podstawowym \(2 \pi\)
\(T = 2 \pi\)
• Miejscami zerowymi funkcji są liczby postaci \(k \pi\), przy czym \(k\) należy do zbioru liczb całkowitych
\(x_0 = k \pi\), \(k \in C\)\
• Maksima funkcji w punktach
\((\dfrac{\pi}{2} + 2k \pi, 1)\), \(k \in C\)
• Minima funkcji w punktach
\((-\dfrac{\pi}{2} + 2k \pi, -1)\), \(k \in C\)
• Funkcja nie jest różnowartościowa w swojej dziedzinie
• Funkcja jest nieparzysta
Jak powstaje funkcja sin(x) ?
Rysując wykres funkcji sin(x), w kole dla danego kąta rysujemy trójkąt prostokątny, którego pozioma przyprostokątna leży na osi OX ma początek w środku koła, druga przyprostokątna (pionowa) ma początek na okręgu, przeciwprostokątna ma początek w środku koła a koniec na okręgu wyznaczając kąt. Aby narysować wykres funkcji sinus należy odłożyć na oś OX długość okręgu wyznaczoną przez kąt a na osi OY odłożyć długość pionowej przyprostokątnej naszego trójkąta.
Funkcja sinus Wasze opinie