Zbiór to pierwotne pojęcie matematyczne, oznacza to, że pojęcia tego nie definiujemy. Jest to pewna całość złożona z pewnej ilości obiektów, zbiór liczb całkowitych, zbiór długopisów w piórniku, zbiór butów w szafce. Zbiory oznaczamy zawsze wielkimi literami alfabetu. Każdy zbiór składa się z elementów, elementy oznaczamy małymi literami. Szczególnym przypadkiem zbioru jest zbiór pusty, który nie zawiera żadnego elementu.
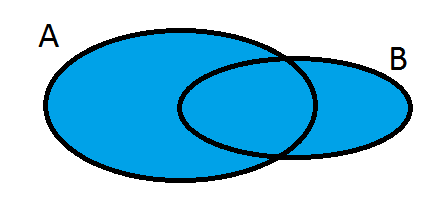
Diagram Venna to diagramy, które umożliwiają przedstawianie w postaci graficznej zależności między zbiorami. Przyjmują postać różnych figur geometrycznych jednak najczęściej są to elipsy. Wzajemne relacje między zbiorami możemy schematycznie przedstawić:
- Zbiór
- różnica zbiorów
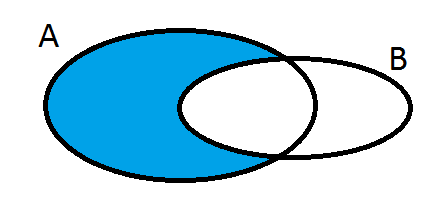
- Zbiór
- przecięcie zbiorów

- Zbiór
- różnica zbiorów
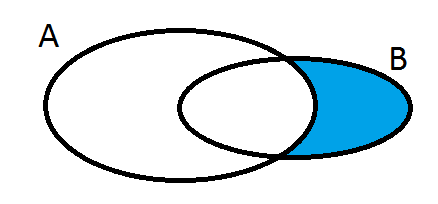
- Zbiór B
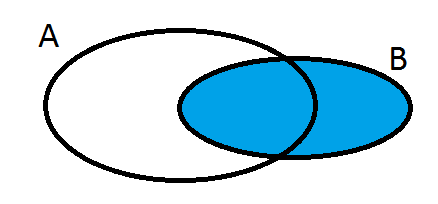
- Zbiór A
- Zbiór
- suma zbiorów
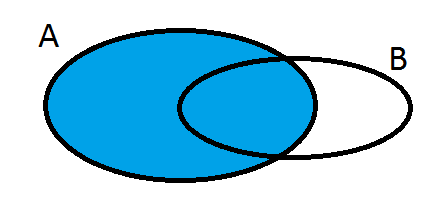
- Zbiór
jest to zbiór pusty
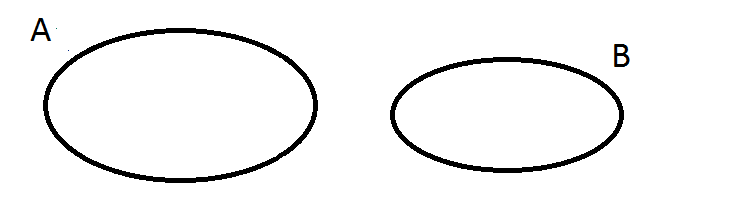
- Zbiór
- dopełnienie zbioru

Prawo rachunku zbiorów:
- przemienność sumy zbiorów A ∪ B = B ∪ A
- przemienność iloczynu zbiorów A ∩ B = B ∩ A
- łączność sumy zbiorów (A ∪ B) ∪ C = A ∪ (B ∪ C)
- rozdzielność iloczynu względem sumy zbiorów A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- rozdzielność sumy względem iloczynu zbiorów A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
- łączność iloczynu zbiorów (A ∩ B) ∩ C = A ∩ (B ∩ C)
- prawa de Morgana dla zbiorów (A ∪ B)' = A' ∩ B' oraz (A ∩ B)' = A' ∪ B'
Zbiory Wasze opinie
Dzięki Za Wytłumaczenie , Teraz mam za co wykarmić rodzinę
spoko
Trzeci rysunek powinien być podpisany B/A, a nie A/B.
Źle zaznaczone działania na zbiorach, bo nie wiadomo co jest domknięte a co otwarte? Linią ciągłą wszystko jest narysowane.