Hiperbolą nazywamy krzywą, która jest zbiorem takich punktów, dla których wartość bezwzględna różnicy odległości tych punktów od dwóch ustalonych punktów (tzw. ognisk) jest stała.
W ogólności, jeżeli ogniska hiperboli znajdują się we współrzędnych \((-c, 0)\) oraz \((c,0)\), to możemy ją opisać równaniem:
\({{x^2 \over a^2} - {y^2 \over b^2}} = 1\)
gdzie: a to połowa odległości między wierzchołkami hiperboli a b to połowa odległości między wierzchołkami urojonymi.
Oczywiście, możemy mieć do czynienia z przypadkiem, gdy \(a=b\). Wówczas nazywamy hiperbolę równoosiową (jej asymptoty są prostopadłe).
Inny związek, który może zajść, to: \(b^2 = c^2 - a^2.\)
Asymptotami hiperboli są osie układu współrzędnych. Dla przypomnienia: asymptota to prosta, do której wykres się zbliża, lecz jej nie dotyka. W ten sposób, oś X jest asymptotą poziomą hiperboli a oś Y asymptotą pionową hiperboli.
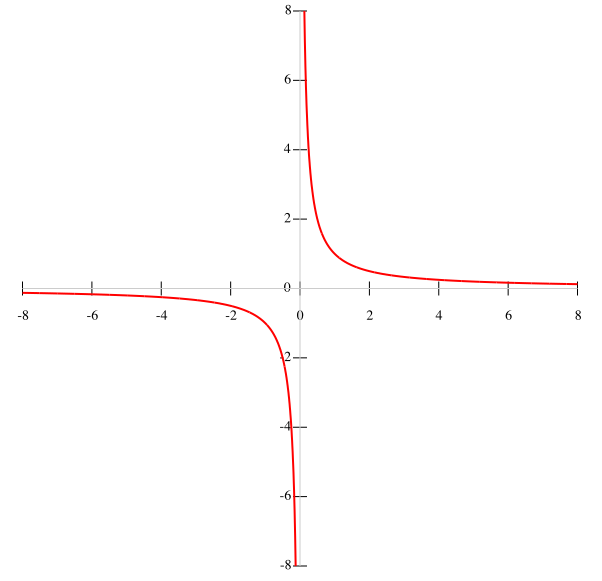
Hiperbola Wasze opinie