Geometria – to najstarszy dział matematyki, w który zajmuję się opisem figur geometrycznych i związków występujących między nimi. Z geometrią związani są najwięksi matematycy świata tacy jak Pitagoras, Tales Arystoteles czy Euklides. Geometrię możemy podzielić na planimetrię (część geometrii, która zajmuję się figurami geometrycznymi na płaszczyźnie) oraz stereometrię (część geometrii, która zajmuję się figurami geometrycznymi w przestrzeni).
Do podstawowych konstrukcji geometrycznych należy:
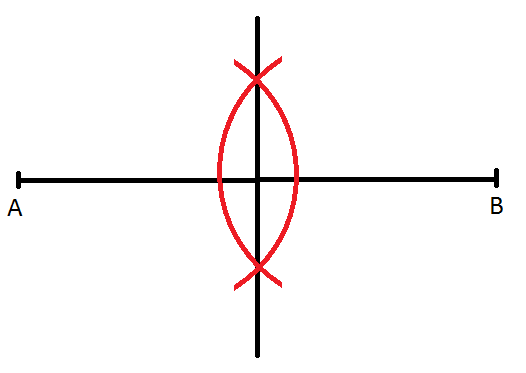
- konstrukcyjny podział odcinka na połowę (symetralna odcinka) – aby podzielić konstrukcyjnie odcinek na połowę należy cyrklem zaznaczyć półokrąg o dowolnym promieniu, ale większym niż połowa długości odcinka, w obu końcach odcinka należy narysować półokrąg o takim samym promieniu. Prosta, która powstanie z przecięcia tych półkoli będzie prostą dzieląca odcinek na połowy.
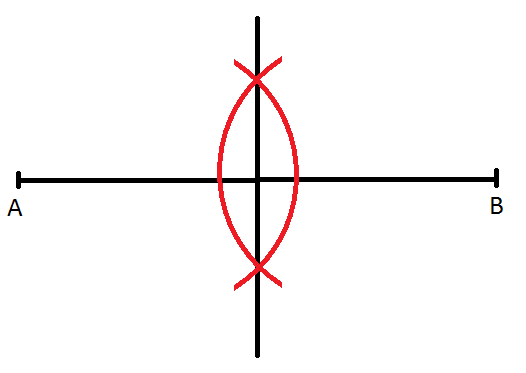
- podział odcinka na n równych części. Aby podzielić odcinek AB na n równych części, należy narysować półprostą k o początku w jednym z końców odcinka AB, następnie za pomocą cyrkla należy odłożyć na półprostej n odcinków dowolnej, ale tej samej długości. Przy użyciu linijki i ekierki należy narysować prostą l równoległą do odcinka AB. Przykładając linijkę wzdłuż prostej l i ekierkę jednym bokiem przyprostokątnym do linijki, a drugim przesuwając należy narysować proste przecinające odcinek AB z prostą k w zaznaczonych odcinkach. Otrzymujemy podział odcinka na n części
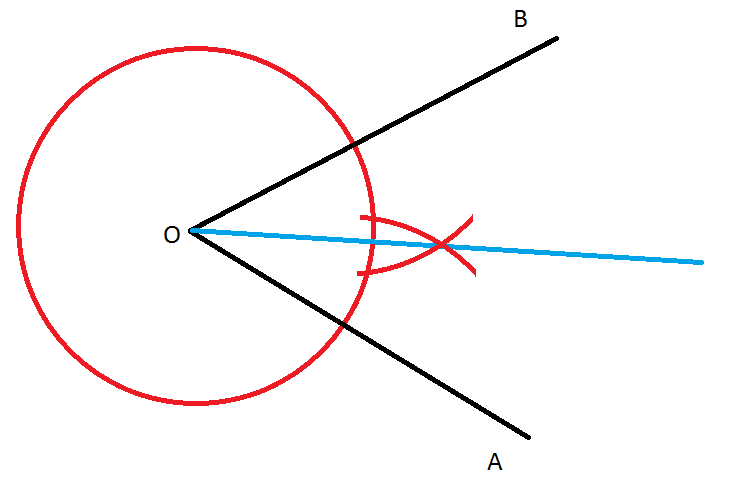
- podział kąta AOB na połowę – konstrukcje tę należy rozpocząć od narysowania dowolnego okręgu o środku w punkcie O (wierzchołku kąta) w punktach przecięcia okręgu z ramionami kąta. Aby to zrobić należy zakreślić 2 łuki o promieniu większym niż połowa tego kąta w punkcie przecięcia okręgu i ramion kąta, najlepiej o promieniu rysowanego koła, połączyć punkt przecięcia narysowanych półkoli i środka okręgu – otrzymana prosta jest dwusieczną kąta.
- konstrukcja prostej prostopadłej do danej prostej l i przechodząca przez punkt A nie leżący na tej prostej – należy narysować dowolny okrąg o środku w punkcie a, o promieniu takim, który będzie przecinał prostą l w dwóch punktach. Następnie należy wyznaczyć symetralną otrzymanego odcinka AB, tak jak opisano wyżej. Otrzymana symetralna będzie prostą prostopadłą przechodzącą przez punkt A.
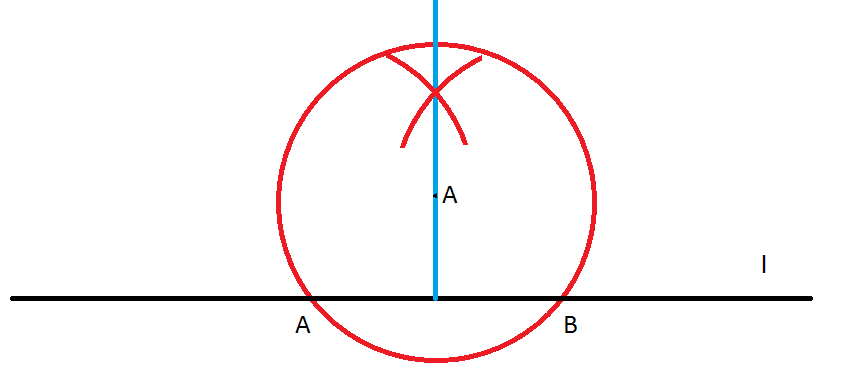
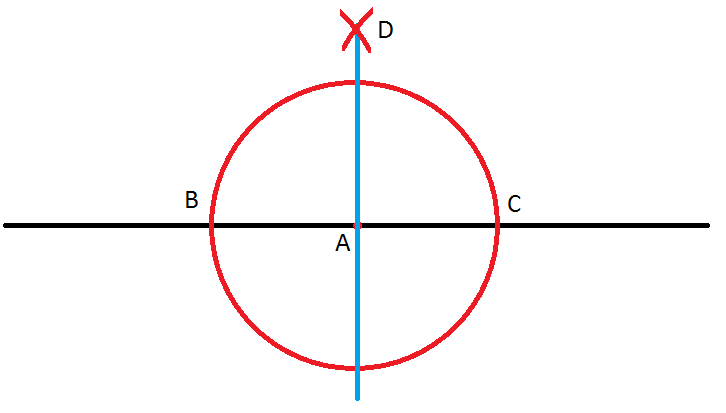
- konstrukcja prostej prostopadłej do danej prostej l i przechodząca przez punkt A leżący na tej prostej – należy narysować dowolny okrąg o środku w punkcie A, zgodnie ze wskazówkami powyżej narysować symetralną otrzymanego odcinka BC.
Geometria Wasze opinie