WIELOMIAN to wyrażenie algebraiczne będące sumą jednomianów.
POSTAĆ ILOCZYNOWA WIELOMIANU to wielomian zapisany w postaci iloczynu czynników, czynnikami tymi są wielomiany niższych stopni.
Przykład 1. Zapisz wielomian w postaci iloczynowej: f(x) = x2 - 9
f(x)= (x-3)(x+3)
Przykład 2. Zapisz wielomian w postaci iloczynowej: g(x) =x3-3x2-8x+4
g(x)=(x+2)(x2-5x+2) bo (x+2)(x2-5x+2)=x3-5x2+2x+2x2-10x+4=x3-3x2-8x+4
RÓWNOŚĆ WIELOMIANÓW wielomian f(x) jest równy wielomianowi g(x) wtedy i tylko wtedy gdy współczynniki stojące przy zmiennych o tych samych samych potęgach są sobie równe
f(x)=ax3+bx2+cx+d
g(x)=ex3+fx2+gx+h
wielomian f(x) jest równy wielomianowi g(x) gdy:
a=e, b=f, c=g oraz d=h
TWIERDZENIE O RESZCIE reszta z dzielenia wielomian f(x) przez dwumian (x-a) jest równa wielomianowi f(a)
TWIERDZENIE BEZOUTE`A pewna liczba a jest pierwiastkiem wielomianu f(x) jeżeli wielomian ten jest podzielny przez dwumian (x-a)
PIERWIASTKI WIELOMIANU (miejsca zerowe) jest to liczba dla której wartość wielomianu jest równa 0
Przykład 1. Oblicz pierwiastki wielomianu f(x)=4x3-18x2+20x-6
f(x)=4x3-18x2+20x-6 = 4x3-4x2-14x2+14x+6x-6=4x2(x-1)-14x(x-1)+6(x-1)=(x-1)(4x2-14x+6)
obliczam pierwiastki równania kwadratowego
∆=b2-4ac
x1\(= {-b - \sqrt{∆} \over 2a}\) x2=\(= {-b + \sqrt{∆} \over 2a}\)
∆=142-4*4*6=100
\( { \sqrt{∆} }=10\)
x1=0,5 x2=3
pierwiastki wielomianu to x1=0,5, x2=3, x3=1 co można zapisać w postaci iloczynowej f(x)=(x-1)(x-3)(x-0,5)
Miejsca zerowe wielomianu czyli pierwiastki wielomianu to takie liczby dla których wielomian jest równy 0
Dzielenie wielomianów odbywa się w analogiczny sposób do dzielenia pisemnego. Jeżeli chcemy podzielić wielomian W(x) = (x2 + 4x - 5) przez wielomian P(x) = (x - 1), gdzie W(x) nazywa się dzielna a P(x) dzielnikiem. Działanie to wykonuje się w następujących krokach:
- dzielimy pierwszy wielomian x2 przez x
- otrzymany wynik wpisujemy nad kreską
- wpisany wynik dzielenia mnożę przez (x - 1), jednocześnie zmieniam znaki na przeciwne i wynik zapisuje pod wielomianem W (x), pamiętając o tym aby zapisywać jednomian pod jednomianem tego samego stopnia
- podkreślamy całe działanie i dodajemy pisemnie, redukujemy jednomiany tego samego stopnia
- spisujemy wartość -5 z wielomianu W(x)
- dzielimy najwyższa potęgę w wielomianie 5x - 5 przez x pochodzący z wielomianu (x - 1)
- wynik dzielenia zapisujemy nad górną kreską
- otrzymany jednomian + 5, mnożę przez dwumian (x - 1)
- ponownie mnożę jak w punkcie 3, wykonujemy to tyle raz, aż uzyskamy samą liczbę
- w naszym przypadku otrzymaliśmy 0 co świadczy o tym, że otrzymaliśmy dzielenie wielomianu bez reszty.
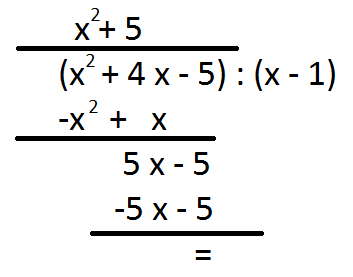
Wielomiany Wasze opinie
Błąd wynik to x+5 bez kwadratu
Ten przykład jest błędnie rozwiązany powinno być x+5