Równanie – dwa wyrażenia algebraiczne połączone znakiem \(=\).
Przykład
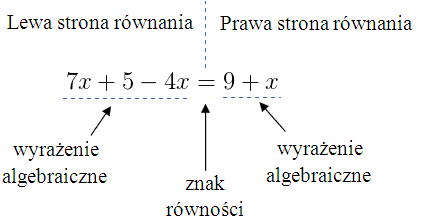
Rozwiązanie równania to obliczenie (znalezienie, zgadnięcie) takiej liczby \(x\), która po podstawieniu do równania i uproszczeniu (wymnożeniu, dodawaniu),da taką samą wartość po lewej i prawej stronie równania.
Rozwiązanie równania polega na przekształcaniu równania do postaci, gdy po jednej stronie równania jest tylko \(x\) (niewiadoma), natomiast po drugiej stronie równania znajduje się liczba (liczba ta jest rozwiązaniem równania).
Przykład
Rozwiązaniem powyższego równania jest:
\(x=2\)
Oznacza to, że po wstawieniu za \(x\) liczby \(2\), otrzymamy po lewej i po prawej stronie równania taką samą wartość.
Wstawmy więc do równania \(7x+5-4x=9+x\) zamiast \(x\), liczbę \(2\).
\(7\cdot 2+5-4\cdot 2=9+2\)
\(14+5-8=11\)
\(19-8=11\)
\(11=11\)
Po lewej i po prawej stronie otrzymaliśmy tą samą wartość, oznacza to, że \(x=2\) jest rozwiązaniem równania \(7x+5-4x=9+x\).
Aby rozwiązać równanie, poza tradycyjnymi operacjami na liczbach, możemy:
- dodawać lub odejmować od obu stron równania takie same wyrażenia,
- mnożyć lub dzielić obie strony równania przez takie same wyrażenia.
Schemat rozwiązywania równań liniowych:
Rozwiązywanie równania będzie polegało na:
1) przeniesieniu wyrażenia z \(x\) na lewą stronę – wykonamy to przez odjęcie od lewej i prawej strony równania wyrażeń z \(x\);
2) przeniesieniu na prawą stronę wyrażeń bez \(x\), czyli wyrazów wolnych np. liczby \(8\) - wykonamy to przez odjęcie od obu stron równania liczby tych liczb;
3) uproszczeniu równania wykonując dodawanie i odejmowanie wyrażeń algebraicznych;
4) podzieleniu równania przez współczynnik znajdujący się przy \(x\).
Wszystkie równania można podzielić ze względu na ilość posiadanych rozwiązań:
- równania oznaczone to takie, które posiadają określoną liczbę rozwiązań (w przypadku równań liniowych będzie to jedno rozwiązanie), np. x=4.
- równania tożsamościowe lub nieoznaczone to takie, które posiadają nieskończenie wiele rozwiązań (dowolna liczba wstawiona za \(x\) jest rozwiązaniem równania), np. 2=2.
- równania sprzeczne to takie, które nie posiadają rozwiązania (nie istnieje taka liczba, która po podstawieniu za \(x\) będzie rozwiązaniem równania), np. 4=2.
Przykładowe zadania
Zad. 1) Rozwiąż równanie
a) \(x+5=7\)
b) \(x-6+5x=11+4x+3\)
c) \(6x-10=4x-2\)
d) \(2x-3=x+5\) Zobacz rozwiązanie
Zad. 2) Podaj ilość rozwiązań równania
a) \(2x=2x\)
b) \(6=7-1\)
c) \(2=6\)
d) \(3x=6\) Zobacz rozwiązanie
Przykład

Rozwiązanie równania to obliczenie (znalezienie, zgadnięcie) takiej liczby \(x\), która po podstawieniu do równania i uproszczeniu (wymnożeniu, dodawaniu),da taką samą wartość po lewej i prawej stronie równania.
Rozwiązanie równania polega na przekształcaniu równania do postaci, gdy po jednej stronie równania jest tylko \(x\) (niewiadoma), natomiast po drugiej stronie równania znajduje się liczba (liczba ta jest rozwiązaniem równania).
Przykład
Rozwiązaniem powyższego równania jest:
\(x=2\)
Oznacza to, że po wstawieniu za \(x\) liczby \(2\), otrzymamy po lewej i po prawej stronie równania taką samą wartość.
Wstawmy więc do równania \(7x+5-4x=9+x\) zamiast \(x\), liczbę \(2\).
\(7\cdot 2+5-4\cdot 2=9+2\)
\(14+5-8=11\)
\(19-8=11\)
\(11=11\)
Po lewej i po prawej stronie otrzymaliśmy tą samą wartość, oznacza to, że \(x=2\) jest rozwiązaniem równania \(7x+5-4x=9+x\).
Aby rozwiązać równanie, poza tradycyjnymi operacjami na liczbach, możemy:
- dodawać lub odejmować od obu stron równania takie same wyrażenia,
- mnożyć lub dzielić obie strony równania przez takie same wyrażenia.
Schemat rozwiązywania równań liniowych:
Rozwiązywanie równania będzie polegało na:
1) przeniesieniu wyrażenia z \(x\) na lewą stronę – wykonamy to przez odjęcie od lewej i prawej strony równania wyrażeń z \(x\);
2) przeniesieniu na prawą stronę wyrażeń bez \(x\), czyli wyrazów wolnych np. liczby \(8\) - wykonamy to przez odjęcie od obu stron równania liczby tych liczb;
3) uproszczeniu równania wykonując dodawanie i odejmowanie wyrażeń algebraicznych;
4) podzieleniu równania przez współczynnik znajdujący się przy \(x\).
Wszystkie równania można podzielić ze względu na ilość posiadanych rozwiązań:
- równania oznaczone to takie, które posiadają określoną liczbę rozwiązań (w przypadku równań liniowych będzie to jedno rozwiązanie), np. x=4.
- równania tożsamościowe lub nieoznaczone to takie, które posiadają nieskończenie wiele rozwiązań (dowolna liczba wstawiona za \(x\) jest rozwiązaniem równania), np. 2=2.
- równania sprzeczne to takie, które nie posiadają rozwiązania (nie istnieje taka liczba, która po podstawieniu za \(x\) będzie rozwiązaniem równania), np. 4=2.
Przykładowe zadania
Zad. 1) Rozwiąż równanie
a) \(x+5=7\)
b) \(x-6+5x=11+4x+3\)
c) \(6x-10=4x-2\)
d) \(2x-3=x+5\) Zobacz rozwiązanie
Zad. 2) Podaj ilość rozwiązań równania
a) \(2x=2x\)
b) \(6=7-1\)
c) \(2=6\)
d) \(3x=6\) Zobacz rozwiązanie
Równania liniowe Wasze opinie
"mnożyć lub dzielić obie strony równania przez takie same wyrażenia." Czyli można mnożyć i dzielić przez niewiadomą oraz mnożyć i dzielić przez 0? Mnożyć i dzielić obustronnie można tylko przez liczbę różną od zera.