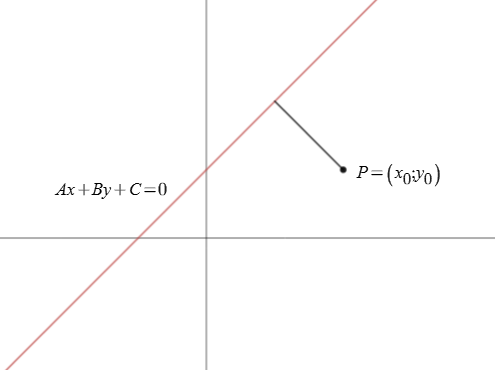
Odległość punktu od prostej - opis

Odległość punktu \(P=(x_0;y_0)\) od prostej o równaniu \(Ax+By+C=0\) jest dana wzorem:

\(d=\dfrac{\left | Ax_0+By_0+C \right |}{\sqrt{A^2+B^2}}\)

Przykład
Oblicz odległość punktu \(A=(3;2)\) od prostej o równaniu \(4x+3y+2=0\).

Podstawiamy do wzoru:
\(d=\dfrac{\left | 4\cdot 3+3\cdot 2+2 \right |}{\sqrt{4^2+3^2}}\)

\(d=\dfrac{\left | 12+6+2 \right |}{\sqrt{16+9}}\)

\(d=\dfrac{\left | 20 \right |}{\sqrt{25}}\)

\(d=\dfrac{20 }{5}\)

\(d=4\)

Przykładowe zadania
Zad. 1) Oblicz odległość punktu od prostej:
a) \(A=(1;1)\) \(2x+6y+2=0\)

b) \(A=(5;7)\) \(x+2y-8=0\)

c) \(A=(-2;-5)\) \(y=2x+5\)

d) \(A=(-1;0)\) \(y=-x-2\)      Zobacz rozwiązanie

Zad. 2) Oblicz odległość dwóch prostych od siebie:
a) \(x+3y+6=0\) \(2x+6y+2=0\)

b) \(3x+2y+6=0\) \(3x+2y-1=0\)

c) \(-5x+10y=0\) \(x-2y+10=0\)

d) \(x+y+6=0\)\(-x-y+7=0\)      Zobacz rozwiązanie