Dwie proste o równaniach kierunkowych:
\(y=a_1x+b_1\) oraz \(y=a_2x+b_2\)
Spełniają jeden z następujących warunków:
- są równoległe, gdy \(a_1=a_2\)
- są prostopadłe, gdy \(a_1\cdot a_2=-1\)
- tworzą kąt ostry \(\varphi\) i \(tg \varphi=\left | \dfrac{a_1-a_2}{1+a_1a_2} \right |\)
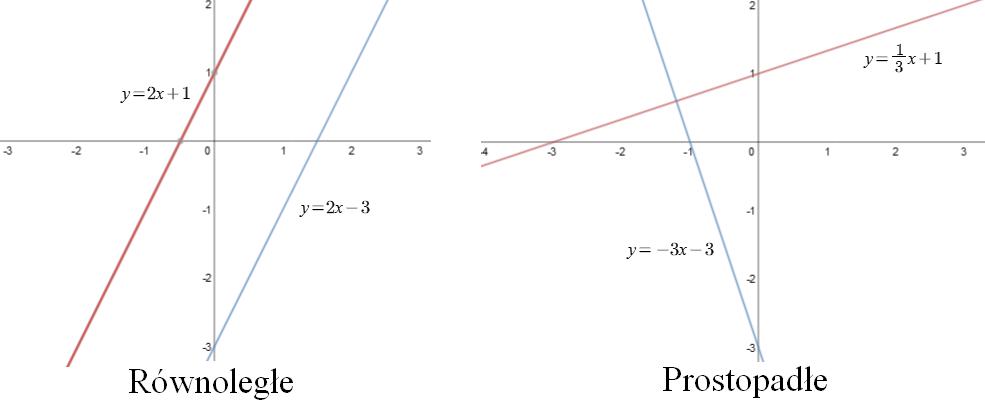
Proste równoległe mają ten sam współczynnik kierunkowy \(a=2\). Proste prostopadłe mają współczynniki kierunkowe odwrotne i przeciwne \(a_1=-3\) oraz \(a_2=\frac{1}{3}\).
Przykładowe zadania
Zad. 1) Które z podanych funkcji są równoległe?
a) \(y=x+7\) i \(y=3x+7\)
b) \(y=4x-5\) i \(y=4x+1\)
c) \(y=\frac{1}{3}x-2\) i \(y=\frac{1}{3}x-4\)
d) \(y=\frac{1}{4}x\) i \(y=-4x+2\) Zobacz rozwiązanie
Zad. 2) Które z podanych funkcji są prostopadłe?
a) \(y=2x+7\) i \(y=\frac{1}{2}x+7\)
b) \(y=-\frac{2}{3}x-5\) i \(y=\frac{3}{2}x\)
c)\(y=3x+2\) i \(y=-3x-\frac{1}{2}\)
d)\(y=-5x-20\) i \(y=\frac{1}{5}x+100\) Zobacz rozwiązanie
Zad. 3) Wyznacz równanie funkcji liniowej, prostopadłej do \(y=x+2\), przechodzącej przez punkt \((4,3)\). Zobacz rozwiązanie
Zad. 4) Wyznacz równanie funkcji liniowej, równoległej do \(y=6x-11\), przechodzącej przez punkt \((12,5)\). Zobacz rozwiązanie
\(y=a_1x+b_1\) oraz \(y=a_2x+b_2\)
Spełniają jeden z następujących warunków:
- są równoległe, gdy \(a_1=a_2\)
- są prostopadłe, gdy \(a_1\cdot a_2=-1\)
- tworzą kąt ostry \(\varphi\) i \(tg \varphi=\left | \dfrac{a_1-a_2}{1+a_1a_2} \right |\)

Proste równoległe mają ten sam współczynnik kierunkowy \(a=2\). Proste prostopadłe mają współczynniki kierunkowe odwrotne i przeciwne \(a_1=-3\) oraz \(a_2=\frac{1}{3}\).
Przykładowe zadania
Zad. 1) Które z podanych funkcji są równoległe?
a) \(y=x+7\) i \(y=3x+7\)
b) \(y=4x-5\) i \(y=4x+1\)
c) \(y=\frac{1}{3}x-2\) i \(y=\frac{1}{3}x-4\)
d) \(y=\frac{1}{4}x\) i \(y=-4x+2\) Zobacz rozwiązanie
Zad. 2) Które z podanych funkcji są prostopadłe?
a) \(y=2x+7\) i \(y=\frac{1}{2}x+7\)
b) \(y=-\frac{2}{3}x-5\) i \(y=\frac{3}{2}x\)
c)\(y=3x+2\) i \(y=-3x-\frac{1}{2}\)
d)\(y=-5x-20\) i \(y=\frac{1}{5}x+100\) Zobacz rozwiązanie
Zad. 3) Wyznacz równanie funkcji liniowej, prostopadłej do \(y=x+2\), przechodzącej przez punkt \((4,3)\). Zobacz rozwiązanie
Zad. 4) Wyznacz równanie funkcji liniowej, równoległej do \(y=6x-11\), przechodzącej przez punkt \((12,5)\). Zobacz rozwiązanie
Para prostych Wasze opinie