Funkcja i jej własności - opis

FUNKCJA to przyporządkowanie każdemu elementowi jednego zbioru dokładnie jednego elementu drugiego zbioru.

Właściwości funkcji:

1. Dziedzina to zbiór tych wszystkich wartości dla których możemy obliczyć wartość funkcji
2. Zbiór wartości są to wszystkie y-ki jakie może osiągnąć funkcja
3. Miejsca zerowe to taki argument x dla którego wartość funkcji wynosi 0
4. Parzystość - funkcja jest parzysta jeżeli jej wykres jest symetryczny względem osi OY
5. Nieparzystość - funkcja jest nieparzysta jeżeli jej wykres jest symetryczny względem punktu (0,0)
6. Różnowartościowość jeżeli dla każdego x funkcja przyjmuje inna wartość (można to łatwo sprawdzić przecinając wykres funkcji prostą i jeżeli prostą tą nie da się przeciąć funkcji w więcej niż jednym punkcie mówimy że nasza funkcja jest różnowartościowa).
7. Maksimum to największa wartość osiągana przez funkcje
8. Minimum to najmniejsza wartość jaka osiąga funkcja
9. Monotoniczność 

• funkcja rosnąca - jeżeli wykres funkcji rośnie
• funkcja malejąca - jeżeli wykres funkcji maleje
• funkcja stała - to taka funkcja której wykres jest równoległy do osi x
• funkcja niemalejąca - to taka której wykres rośnie lub jest stały
• funkcja nierosnąca - to taka której wykres maleje lub jest stały

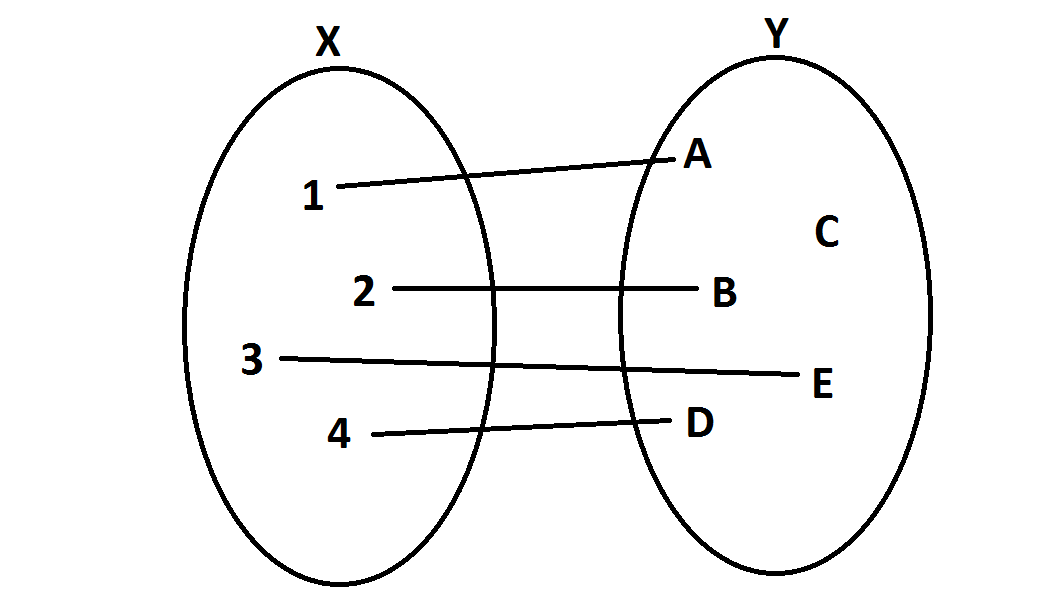
INIEKCJA jest to taka funkcja w której każdy element przeciwdziedziny przyjmowany jest co najwyżej jeden raz.

SURJEKCJA to tzw funkcja "na" - funkcja której elementy dziedziny przyjmują wszystkie wartości przeciwdziedziny

BIJEKCJA funkcje nazywamy  bijekcją jeżeli jest jednocześnie iniekcją i surjekcją. Czyli każdemu elementowi dziedziny odpowiada dokładnie jeden element przeciwdziedziny a także każdemu elementowi przeciwdziedziny odpowiada dokładnie jakiemuś jednemu argumentowi.