Funkcja parzysta 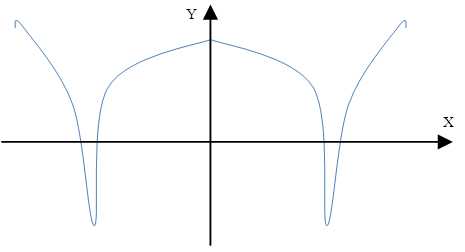
Funkcja nieparzysta
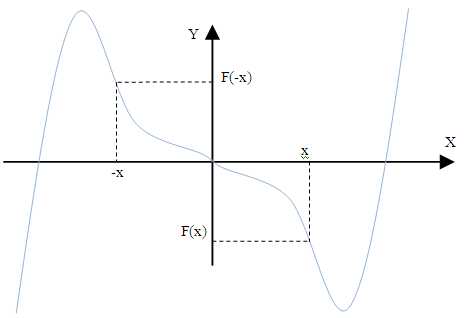

Funkcję \(f\) określoną w zbiorze \(D_f\) nazywamy parzystą jeżeli dla każdego \(x \in D_f\) liczba \(-x \in D_f\) oraz \(f(-x) = f(x)\)
\(\bigwedge\limits_{x \in D_f}[ - x \in D_f ∧ f(-x) = f(x)]\)
Funkcja \(f\) jest parzysta wtedy i tylko wtedy, gdy oś \(OY\) jest osią symetrii wykresu tej funkcji.
Przykłady funkcji parzystych:
• \(f(x)= cos \: x\)
• \(f(x)=\left | x \right |\)
• \(f(x)= x^2\:\: ; \: f(x)=x^4\)
Przykłady funkcji parzystych:
• \(f(x)= cos \: x\)
• \(f(x)=\left | x \right |\)
• \(f(x)= x^2\:\: ; \: f(x)=x^4\)
Funkcja nieparzysta

Funkcję \(f\) określoną w zbiorze \(D_f\) nazywamy nieparzystą jeżeli dla każdego \(x \in D_f\) liczba \(-x \in D_f\) oraz \(f(-x) = - f(x)\)
\(\bigwedge\limits_{x \in D_f}[ - x \in D_f \wedge f(-x) = -f(x)]\)
Funkcja \(f\) jest nieparzysta wtedy i tylko wtedy, gdy punkt \(O = (0,0)\) jest środkiem symetrii wykresu tej funkcji.
Przykłady funkcji parzystych:
• \(f(x)= sin \: x\)
• \(f(x)=2x\: \: ; \: f(x)=4x\)
• \(f(x)= x^3\:\: ; \: f(x)=x^5\)
przykład sprawdzania czy funkcja jest parzysta, czy nieparzysta:
1) niech dana będzie funkcja \(f(x)=7x^2+4\)
najpierw wyznaczamy dziedzinę funkcji \(D_f=R\)
następnie sprawdzamy czy \(f(x)=f(-x)\)
\(f(-x)=7(-x)^2+4=7x^2+4=f(x)\)
tak więc funkcja jest funkcją parzystą, oznacza to również, że wykres funkcji jest symetryczny względem osi OY
2) niech dana będzie funkcja \(f(x)=\dfrac{2x}{x^2+7}\)
najpierw wyznaczamy dziedzinę funkcji \(D_f=R\)
następnie sprawdzamy czy \(f(x)=f(-x)\)
\(f(-x)=\dfrac{2(-x)}{(-x)^2+7}=\dfrac{-2x}{x^2+7}=-\dfrac{2x}{x^2+7}=-f(x)\)
tak więc podana funkcja spełnia warunek \(f(-x)=-f(x)\) co oznacza, że funkcja jest nieparzysta, na wykresie oznacza to, że jest symetryczna względem punktu \(O = (0,0)\)
Przykłady funkcji parzystych:
• \(f(x)= sin \: x\)
• \(f(x)=2x\: \: ; \: f(x)=4x\)
• \(f(x)= x^3\:\: ; \: f(x)=x^5\)
przykład sprawdzania czy funkcja jest parzysta, czy nieparzysta:
1) niech dana będzie funkcja \(f(x)=7x^2+4\)
najpierw wyznaczamy dziedzinę funkcji \(D_f=R\)
następnie sprawdzamy czy \(f(x)=f(-x)\)
\(f(-x)=7(-x)^2+4=7x^2+4=f(x)\)
tak więc funkcja jest funkcją parzystą, oznacza to również, że wykres funkcji jest symetryczny względem osi OY
2) niech dana będzie funkcja \(f(x)=\dfrac{2x}{x^2+7}\)
najpierw wyznaczamy dziedzinę funkcji \(D_f=R\)
następnie sprawdzamy czy \(f(x)=f(-x)\)
\(f(-x)=\dfrac{2(-x)}{(-x)^2+7}=\dfrac{-2x}{x^2+7}=-\dfrac{2x}{x^2+7}=-f(x)\)
tak więc podana funkcja spełnia warunek \(f(-x)=-f(x)\) co oznacza, że funkcja jest nieparzysta, na wykresie oznacza to, że jest symetryczna względem punktu \(O = (0,0)\)
Parzystość i nieparzystość funkcji - jak stosować w praktyce?