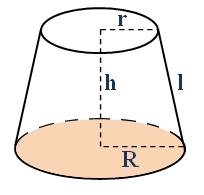
Wzór na objętość stożka ściętego ma postać:\(V = \dfrac{\pi}{3} h (R^2 + R r + r^2)\)
Wyjaśnienie symboli:
\(V\) - objętość stożka ściętego
\(h\) - wysokość stożka ściętego
\(R\), \(r\) - promienie podstaw stożka ściętego
W stożku ściętym obie podstawy są równoległe względem siebie
Wzór na objętość stożka ściętego - jak stosować w praktyce?