Funkcję liniową określamy wzorem:
lub
Funkcja liniowa posiada dwie główne postaci
Równanie ogólne prostej:
Równanie kierunkowe funkcji liniowej:
\(a\) - współczynnik kierunkowy \(a=tg \alpha \) gdzie \(\alpha\) to kąt pomiędzy wykresem funkcji, a osią OX.
\(b\) - wyraz wolny.
Monotoniczność dla: \(a>0\) – rosnąca ; \(a<0\) – malejąca ; \(a=0\) - stała
Współczynnik \(b\) wyznacza punkt przecięcia z osią OY\((0;b)\)
Wykres funkcji liniowej jest linią prostą
Przykład 1
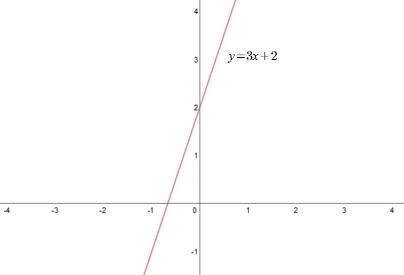
Przykład 2
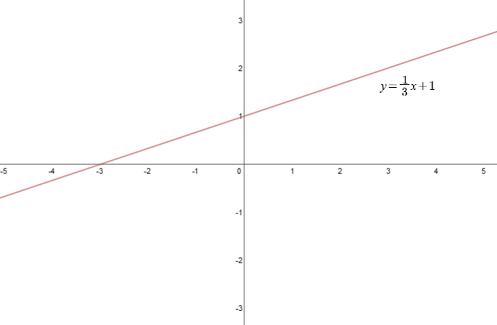
Równanie kierunkowe prostej o współczynniku kierunkowym \(a\), która przechodzi przez punkt \(P=(x_0,y_0)\), wyznacza się z następującego wzoru:
\(y=a(x-x_0)+y_0\)
Przykład
Wyznacz równanie prostej o współczynniku \(a=2\) i przechodzącej przez punkt \(A=(3,5;7)\):
Wstawiamy do wzoru w miejsce \(a\) liczbę 2, natomiast za \(x_0\) podstawiamy 3,5, za \(y_0\) podstawiamy 7. Do wyliczenia pozostaje współczynnik \(b\), więc:
\(y=a(x-x_0)+y_0\)
\(y=2\cdot(x-3,5)+7\)
\(y=2x-7+7\)
\(y=2x\)
Odpowiedź: Szukany wzór funkcji to \(y=2x\).
Przykładowe zadanie
Zad. 1) Dla podanych funkcji podaj współczynnik kierunkowy, miejsce przecięcia z osią OY, monotoniczność:
a) \(y=2x+7\)
b) \(y=\frac{2}{5}x+4\)
c) \(y=-x-7\)
d) \(y=-\frac{1}{2}x+5\) Zobacz rozwiązanie
Zad. 2) Narysuj wykres funkcji liniowej, podaj punkt przecięcia się wykresu z osią OY oraz monotoniczność:
a) \(y=x+1\)
b) \(y=\frac{1}{3}x-1\)
c) \(y=-2x+3\)
d) \(y=-\frac{1}{2}x-2\) Zobacz rozwiązanie
Funkcja liniowa Wasze opinie