Wartość bezwzględna - interpretacja geometryczna - opis

Wartość bezwzględną można przedstawić na osi liczbowej, określając odległość danego punktu od środka osi (punktu zero). Ogólnie mówiąc, wartość bezwzględna z liczby jest równa odległości tej liczby od zera na osi liczbowej. Przykładowo liczba \(-x\) oraz liczba \(x\) są oddalone od zera na osi liczbowej o odległość równą \(x\):



Dlatego      \(|-x|=x\)   oraz   \(|x|=x\).



W przypadku, gdy mamy wartość bezwzględną różnicy dwóch punktów, to określamy odległość między tymi punktami.



Przykład - Jaka odległość jest miedzy punktem \(7\) a punktem \(4\)?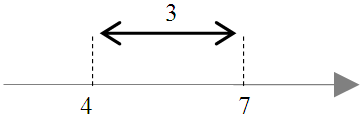



\(|4-7|=3\) oraz \(|7-4|=3\)

Szukana odległość wynosi \(3\).

Wartość bezwzględną można przedstawić jako funkcję. Wykres takiej funkcji najczęściej będzie miał kształt litery V i będzie nad osią OX.

Wykres funkcji \(y=|x|\) wygląda następująco: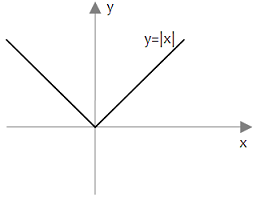



Na wszystkie wykresy tego typu mamy wzór:

\(y=|x-p|+q\)

gdzie wartości \(p\) oraz \(q\) oznaczają punkt załamania wykresu \((p;q)\). Jeśli mamy wzór funkcji o równaniu:

\(y=|x-2|+3\)

\(p=2\)  ;  \(q=3\)

to aby go narysować, należy powyższy wykres (y=|x|) przesunąć o \(2\) w prawo oraz \(3\) do góry.

W przypadku funkcji \(y=\left | f(x) \right |\), czyli dowolnej funkcji, aby narysować jej wykres, najpierw należy narysować wykres samej funkcji \(f(x)\), a następnie część wykresu, który znajduje się poniżej osi OX, odbić na drugą stronę tej osi (na zasadzie lustrzanego odbicia ale tylko dolnej części wykresu)

Przykład

Wykres funkcji \(y=|x^2-4|\) powstaje najpierw z wykresu \(y=x^2-4\), a następnie część pod osią OX jest odbijana na drugą stronę osi: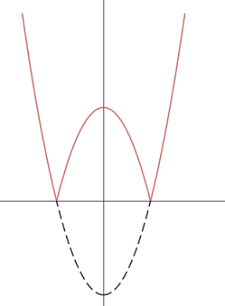



Przykładowe zadania

Zad. 1) Rozwiąż równanie, przedstawiając na osi liczbowej:

a) \(|x|=5\)     b) \(|x-4|=2\)     c) \(|x-3|=1\)     d) \(|x-2|=3\)

e) \(|x-1|=0\)     f) \(|x+2|=4\)     g) \(|x+3|=-1\)     h) \(|x+4|=2\)     Zobacz rozwiązanie

Zad. 2) Rozwiąż nierówność, korzystając z interpretacji geometrycznej na osi liczbowej:

a) \(|x|<5\)     b) \(|x-4|>2\)     c) \(|x-3| \geqslant 1\)     d) \(|x-2| \leqslant 3\)

e) \(|x-1|>0\)     f) \(|x+2|>4\)     g) \(|x+3| \geqslant -1\)     h) \(|x+4| \leqslant 2\)     Zobacz rozwiązanie


Zad. 3) Naszkicuj wykres funkcji:

a) \(y=|x|-2\)     b) \(y=|x+3|-5\)     c) \(y=|x-1|\)     d) \(y=|x-2|+3\)     Zobacz rozwiązanie

Zad. 4) Naszkicuj wykres funkcji:

a) \(y=|x^2-3|\)     b) \(y=|x^2-1|-2\)     Zobacz rozwiązanie