Naszkicuj wykres funkcji:
a) \(y=|x^2-3|\) b) \(y=|x^2-1|-2\)
Rozwiązanie
a)
\(y=|x^2-3|\)
Rysowanie wykresu najłatwiej zacząć od narysowania wykresu bez wartości bezwzględnej, następnie część wykresu, który znajduje się pod osią OX, należy odbić na druga stronę osi. Często naszkicowanie wykresu ułatwia najpierw zrobienie tabelki.
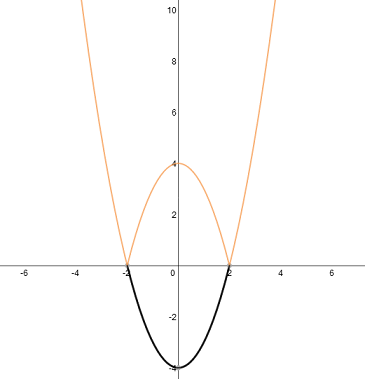
b)
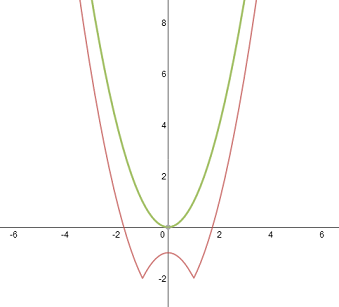
\(y=|x^2-1|-2\)
Następujący wykres najłatwiej narysować zaczynając od naszkicowania wykresu funkcji \(y=x^2-1\) następnie cześć wykresu, który znajduje się pod osią OX, należy odbić na górną część osi. Tak otrzymany wykres przesuwamy o dwa oczka w dół, ponieważ w końcowej postaci wykresu mamy \(-2\). Naszkicowanie wykresu często ułatwia tabelka.
a) \(y=|x^2-3|\) b) \(y=|x^2-1|-2\)
Rozwiązanie
a)
\(y=|x^2-3|\)
Rysowanie wykresu najłatwiej zacząć od narysowania wykresu bez wartości bezwzględnej, następnie część wykresu, który znajduje się pod osią OX, należy odbić na druga stronę osi. Często naszkicowanie wykresu ułatwia najpierw zrobienie tabelki.

b)
\(y=|x^2-1|-2\)
Następujący wykres najłatwiej narysować zaczynając od naszkicowania wykresu funkcji \(y=x^2-1\) następnie cześć wykresu, który znajduje się pod osią OX, należy odbić na górną część osi. Tak otrzymany wykres przesuwamy o dwa oczka w dół, ponieważ w końcowej postaci wykresu mamy \(-2\). Naszkicowanie wykresu często ułatwia tabelka.
Jak obliczyć wartość bezwzględna - interpretacja geometryczna – zadanie 4 - wyniki