Rozwiąż równanie, przedstawiając na osi liczbowej:
a) \(|x|=5\) b) \(|x-4|=2\) c) \(|x-3|=1\) d) \(|x-2|=3\)
e) \(|x-1|=0\) f) \(|x+2|=4\) g) \(|x+3|=-1\) h) \(|x+4|=2\)
Rozwiązanie
a)
\(|x|=5\)
\(|x-0|=5\)
Oznacza to, że szukamy liczb, których odległość od liczby \(0\) na osi wynosi 5:

Wynikiem są liczby \(-5\) oraz \(5\).
Odpowiedź: Rozwiązaniem równania jest \(x=-5\) lub \(x=5\).
b)
\(|x-4|=2\)
Szukamy liczb, które od liczby 4 są oddalone o 2:

Wynikiem są liczby \(2\) oraz \(6\).
Odpowiedź: Rozwiązaniem równania jest \(x=2\) lub \(x=6\).
c)
\(|x-3|=1\)
Szukane liczby są oddalone o 1 od liczby 3:

Wynikiem są liczby \(2\) oraz \(4\).
Odpowiedź: Rozwiązaniem równania jest \(x=2\) lub \(x=4\).
d)
\(|x-2|=3\)
Szukane liczby są oddalone o 3 od liczby 2:

Wynikiem są liczby \(-1\) oraz \(5\).
Odpowiedź: Rozwiązaniem równania jest \(x=-1\) lub \(x=3\).
e)
\(|x-1|=0\)
Szukane liczby są oddalone o 0 od liczby 1:

Wynikiem jest liczba \(1\).
Odpowiedź: Rozwiązaniem równania jest \(x=1\).
f)
\(|x+2|=4\)
\(|x-(-2)|=4\)
Szukane liczby są oddalone o 4 od liczby \(-2\):

Wynikiem są liczby \(-5\) oraz \(2\).
Odpowiedź: Rozwiązaniem równania jest \(x=-5\) lub \(x=2\).
g)
\(|x+3|=-1\)
Wartość bezwzględna nie może przyjmować wartości ujemnych. W tym przykładzie wartość bezwzględna miałaby być równa \(-1\), co jest sprzeczne. Oznacza to, że całe równanie nie ma rozwiązania.
Odpowiedź: Podane równanie nie ma rozwiązania.
h)
\(|x+4|=2\)
\(|x-(-4)|=2\)
Szukane liczby są oddalone o 2 od liczby \(-4\):
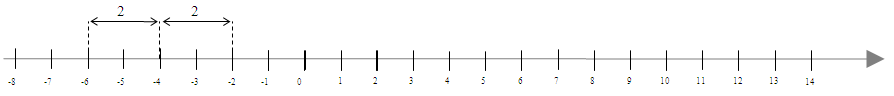
Wynikiem są liczby \(-5\) oraz \(-2\).
Odpowiedź: Rozwiązaniem równania jest \(x=-5\) lub \(x=-2\).
Zadanie 2
Zadanie 3
Zadanie 4
Jak obliczyć wartość bezwzględna - interpretacja geometryczna – zadanie 1 - wyniki