Wartość bezwzględna - interpretacja geometryczna – Zadanie 2 obliczenia

Rozwiąż nierówność, korzystając z interpretacji geometrycznej na osi liczbowej:

a) \(|x|<5\)     b) \(|x-4|>2\)     c) \(|x-3| \geqslant 1\)     d) \(|x-2| \leqslant 3\)

e) \(|x-1|>0\)     f) \(|x+2|>4\)     g) \(|x+3| \geqslant -1\)     h) \(|x+4| \leqslant 2\)


Rozwiązanie

a)
\(|x|<5\)

\(|x-0|<5\)

Szukane są liczby, których odległość na osi liczbowej od liczby \(0\) jest mniejsza niż \(5\):



Odpowiedź: Szukane rozwiązanie to \(x \epsilon (-5;5)\).

b)
\(|x-4|>2\)

Szukamy liczb oddalonych o więcej niż 2 od liczby 4 na osi liczbowej:



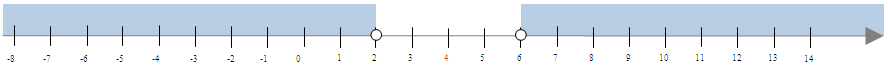
Odpowiedź: Szukane rozwiązanie to \( x\epsilon (-\infty;2) \cup (6;+\infty)\).

c)
\(|x-3| \geqslant 1\)

Szukane są liczby, które od liczby 3 są oddalone dokładnie lub więcej niż 1:



Odpowiedź: Szukane rozwiązanie to \( x\epsilon \left (-\infty;2\right \rangle \cup \left \langle 4;+\infty\right )\).

d)
\(|x-2| \leqslant 3\)

Szukane liczby są oddalone od 2 o odległość mniejszą lub równą 3:



Odpowiedź: Szukane rozwiązanie to \( x\epsilon \left \langle -1;5\right \rangle\).

e)
\(|x-1|>0\)

Szukane liczby są oddalone od 1 o odległość większą niż 0. Ważne, aby pamiętać, że odległość ma być większa od zera, a nie równa. Sama liczba 1 nie należy do rozwiązania, ponieważ jest oddalona od liczby 1 o zero, a ma być więcej niż zero.



Odpowiedź: Szukane rozwiązanie to \( x\epsilon (-\infty;1) \cup (1;+\infty)\).

f)
\(|x+2|\geqslant4\)

\(|x-(-2)| \geqslant4\)

Szukane liczby są oddalone od \(-2\) o odległość większą niż 4:



Odpowiedź: Szukane rozwiązanie to \(x\epsilon \left ( -\infty;-6\right \rangle \cup\left \langle2;+\infty\right )\).

g)
\(|x+3| \geqslant -1\)

\(|x-(-3)| \geqslant -1\)

Szukane liczby są oddalone od liczby \(-3\) o odległość większą lub równą \(-1\):



Wartość bezwzględna ma być większa niż \(-1\). Jest to zawsze prawdziwe twierdzenie. Oznacza to, że rozwiązaniem jest zbiór wszystkich liczb rzeczywistych.

Odpowiedź: Szukane rozwiązanie to \( x\epsilon (-\infty;+\infty)\).

h)
\(|x+4| \leqslant 2\)

\(|x-(-4)| \leqslant2\)

Szukane liczby są oddalone od liczby \(-4\) o odległość mniejszą lub równą 2:



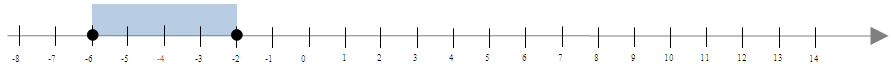
Odpowiedź: Szukane rozwiązanie to \( x\epsilon \left \langle -6;-2 \right \rangle\). 


Zadanie 1 

Zadanie 3 

Zadanie 4