Wartość bezwzględna (moduł) - opis

Wartość bezwzględna zwraca dodatnią wartość z liczby. Często wartość bezwzględną nazywa się modułem lub wartością absolutną.

Wartość bezwzględna z dodatniej liczby to ta sama liczba, np.:

\(\begin{matrix}|2|=2 & |0|=0& |15|=15\\ \\
\left |7\dfrac{1}{2} \right |=7\dfrac{1}{2} & |\sqrt{0,1}|=\sqrt{0,1} & |\dfrac{5}{9}|=\dfrac{5}{9}\\ \\
\left | \dfrac{1}{2}+\dfrac{3}{71} \right |=\dfrac{1}{2} + \dfrac{3}{71} \:\:\:\:\:& |-\sqrt{0,1} + 10|=-\sqrt{0,1} + 10 & \:\:\:\:\:\:\left |-\dfrac{1}{9} + 2\right |=-\dfrac{1}{9} + 2 \end{matrix}\)

Wartość bezwzględna z liczby ujemnej, zwraca liczbę przeciwną (ze zmienionym znakiem), np.:

\(\begin{matrix} |-2|=2 & |-10|=10 & |-125|=125 \\ \\
\left |-7\dfrac{1}{2} \right | =7\dfrac{1}{2} & |-\sqrt{0,1}|=\sqrt{0,1} & \left |-\dfrac{3}{7}\right |=\dfrac{3}{7} \\ \\
\left | -\dfrac{1}{3}-\dfrac{3}{4} \right | =\dfrac{1}{3} + \dfrac{3}{4} \:\:\:\:\:\:\: & \left | \sqrt{0,1} - 10\right |=-\sqrt{0,1} + 10 &\:\:\:\:\:\: \left |-\dfrac{1}{7} - 2\right |=\dfrac{1}{7} + 2 \end{matrix} \)

Definicja

Wartość bezwzględną określa się wzorem:

\(|x|=\left\{\begin{matrix}

x \:\:\:\:\: dla \: x\geqslant 0 \\

-x \:\:\: dla \: x< 0 \\

\end{matrix}\right.\)

Jeśli pod wartością bezwzględną mamy dwie liczby odejmowane od siebie to nie wolno mam rozpatrywać ich oddzielnie. Trzeba obliczyć ich wartość a dopiero obliczyć z nich wartość bezwzględną. Dokładniej o rozwiązywaniu równań i nierówności z wartością bezwzględną opowiemy w oddzielnym artykule.

W interpretacji geometryczne, wartość bezwzględna podaje nam odległość danej liczby od wartości \(0\) na osi liczbowej.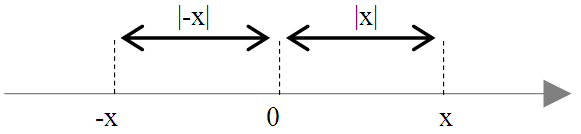



Własności wartości bezwzględnej

\(|x|\geqslant 0\)

\(|x|=|-x|\)

\(|x|=\sqrt{x^2}\)

\(|x\cdot y|=|x|\cdot |y|\)

\(\left | \dfrac{x}{y} \right |=\dfrac{|x|}{|y|}, \:\:\: dla \:y\neq0\)

\(|x-y|=|y-x|\)

\(|x-y|=0\Leftrightarrow x=y\)

\(|x-y|\leqslant |x-z|+|z-y|\)

Przykładowe zadania

Zad. 1) Oblicz wartość bezwzględną z następujących liczb:

a) \(|3|\)     b) \(|-5|\)     c) \(|220|\)     d) \(|-0,2|\)     Zobacz rozwiązanie

Zad. 2) Oblicz

a) \(|9-5|\)     b) \(|-3+11|\)     c) \(|3-2\cdot 2|\)     d) \(|-7+1|\)      Zobacz rozwiązanie

Zad. 3) Oblicz wartość wyrażenia:

a)     \( \left | |2-7|-6 \right |\)     b) \( |3-4|\cdot |-6\cdot (-2)|\)     c) \( |2|-|-8| \)

d) \(\left | \dfrac{|5-|7-1||}{|(|-2|+|9-3|)|-9} \right |\)     Zobacz rozwiązanie