Zbiór wartości funkcji
Zbiór wartości funkcji inaczej zwany przeciwdziedziną funkcji lub zbiór y-ów, są to liczby, które wyjdą nam po wstawieniu do wzoru funkcji f(x) argumentów (x) z dziedziny funkcji. Najczęściej zbiór funkcji zapisujemy symbolami \(ZW\), \(Zf\), przykłady zapisu zbioru wartości: \(ZW=R\) lub \(Zf=\:<-3;+\infty)\). Jeżeli natomiast mamy dany tylko wykres funkcji np.
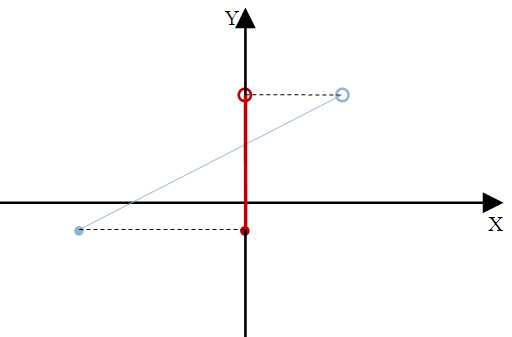
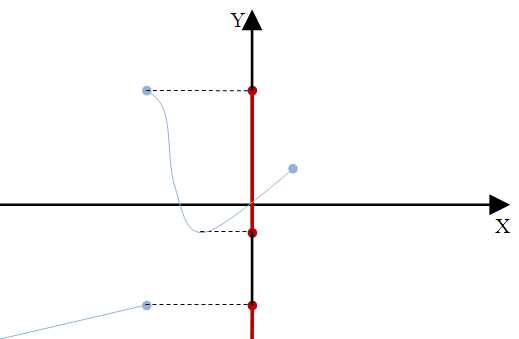
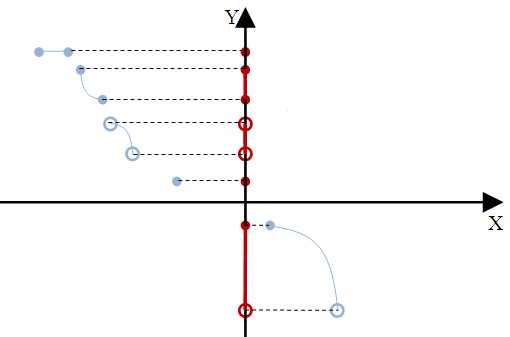
Na przykładach powyżej na czerwono oznaczono zbiór wartości funkcji, na niebiesko wykres funkcji.
Przykład
Odczytaj z wykresu zbiór wartości funkcji:
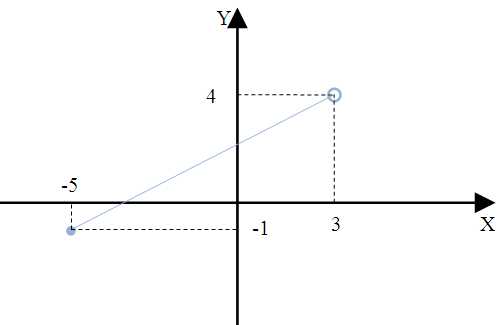
Odpowiedź: Zbiór wartości to \(ZW=\:<-1;4)\)
Przykład
Wyznacz zbiór wartości funkcji \(f(x)=2x^2+7\) dla \(x\: \epsilon \: \{-2;-1;0;1;2\}\).
W takim przypadku zbiór wartości określamy zawsze podstawiając wszystkie x-sy (argumenty) do wzoru, wyniki to zbiór wartości.
\(f(-2)=2\cdot (-2)^2+7=2\cdot4+7=15\)
\(f(-1)=2\cdot (-1)^2+7=2\cdot 1+7=9\)
\(f(0)=2\cdot 0^2+7=2\cdot 0+7=7\)
\(f(2)=2\cdot 2^2+7=2\cdot4+7=15\)
\(f(1)=2\cdot 1^2+7=2\cdot 1+7=9\)
Odpowiedź
Zbiór wartości wynosi \(ZW=\{7;9;15\}\)

Odpowiedź: Zbiór wartości to \(ZW=\:<-1;4)\)
Przykład
Wyznacz zbiór wartości funkcji \(f(x)=2x^2+7\) dla \(x\: \epsilon \: \{-2;-1;0;1;2\}\).
W takim przypadku zbiór wartości określamy zawsze podstawiając wszystkie x-sy (argumenty) do wzoru, wyniki to zbiór wartości.
\(f(-2)=2\cdot (-2)^2+7=2\cdot4+7=15\)
\(f(-1)=2\cdot (-1)^2+7=2\cdot 1+7=9\)
\(f(0)=2\cdot 0^2+7=2\cdot 0+7=7\)
\(f(2)=2\cdot 2^2+7=2\cdot4+7=15\)
\(f(1)=2\cdot 1^2+7=2\cdot 1+7=9\)
Odpowiedź
Zbiór wartości wynosi \(ZW=\{7;9;15\}\)
Zbiór wartości funkcji Wasze opinie