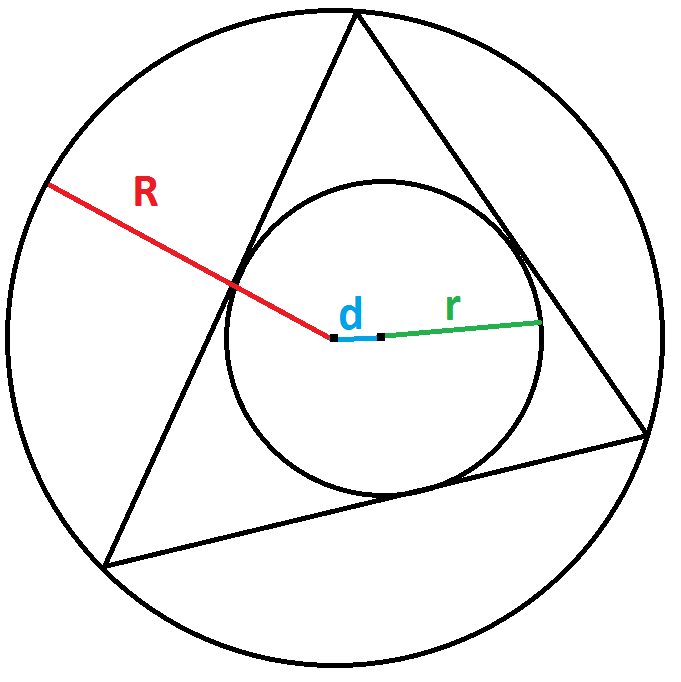
Twierdzenie Eulera to twierdzenie opisujące zależności pomiędzy okręgiem wpisanym i opisanym w trójkąt. Odległość pomiędzy środkiem okręgu wpisanego w trójkąt i środkiem okręgu opisanego na trójkącie wyraża się w następującej zależności:
\(d^2=R(R-2r)\)
gdzie d to odległość pomiędzy środkami okręgu opisanego i wpisanego w trójkąt, R to długość promienia okręgu opisanego na trójkącie, r to promień okręgu wpisanego w trójkąt
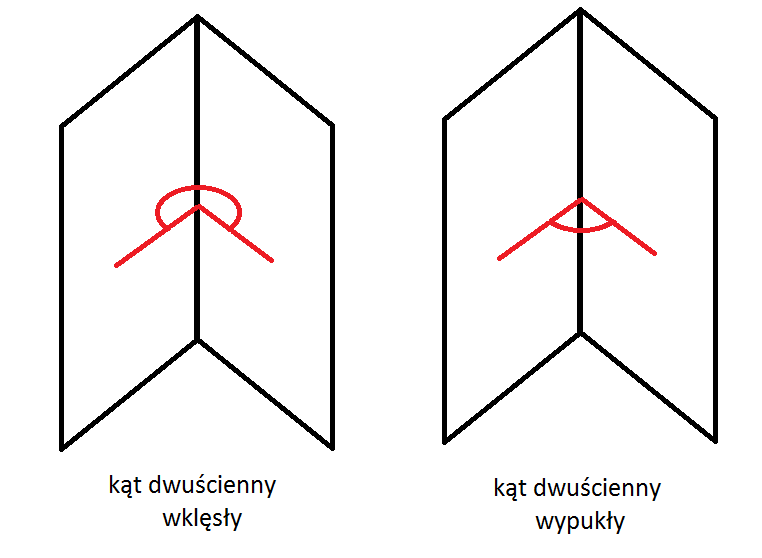
Kąt dwuścienny to kąt między dwoma sąsiednimi ścianami. Aby wyznaczyć kąt dwuścienny należy wyznaczyć prostą powstałą z przecięcia się ścian i na obydwóch płaszczyznach ścian wyróżnić proste (półproste) prostopadłe do prostej otrzymanej z przecięcia ścian. Kąt dwuścienny to kąt pomiędzy otrzymanymi dwoma półprostymi. Otrzymano 2 rodzaje katów dwuściennych:
- kąt dwuścienny wklęsły to kąt, który ma miarę większą niż 180°
- kąt dwuścienny wypukły to kąt mniejszy niż 180°
Twierdzenie Eulera Wasze opinie