Wartość bezwzględna - interpretacja geometryczna – Zadanie 3 obliczenia

Naszkicuj wykres funkcji:

a) \(y=|x|-2\)     b) \(y=|x+3|-5\)     c) \(y=|x-1|\)     d) \(y=|x-2|+3\)

Rozwiązanie

a)                                           
\(y=|x|-2\)

opierając się na wzorze \(y=|x-p|+q\) ustalamy \((p;q)\)

\(y=|x-0|-2\)

więc \((p;q)=(0;-2)\) oznacza to, że wzór funkcji \(y=|x|\) przesuwamy o 2 w dół:



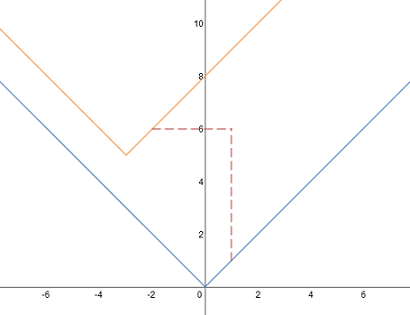
b)
\(y=|x+3|+5\)

opierając się na wzorze \(y=|x-p|+q\) ustalamy \((p;q)\)

\(y=|x-(-3)|+5\)

więc \((p;q)=(-3;5)\) oznacza to, że wzór funkcji \(y=|x|\) przesuwamy o 5 w górę oraz o 3 w lewo:



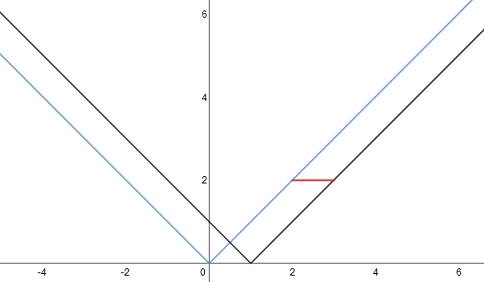
c)
\(y=|x-1|\)

opierając się na wzorze \(y=|x-p|+q\) ustalamy \((p;q)\)

\(y=|x-1|+0\)

więc \((p;q)=(1;0)\) oznacza to, że wzór funkcji \(y=|x|\) przesuwamy o 1 w prawo:



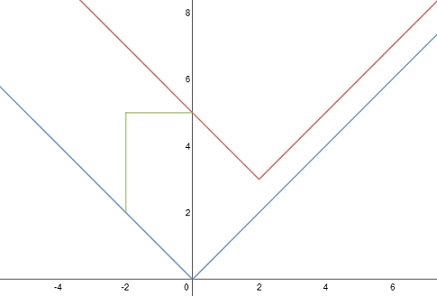
d)
\(y=|x-2|+3\)

opierając się na wzorze \(y=|x-p|+q\) ustalamy \((p;q)\)

\(y=|x-2|+3\)

więc \((p;q)=(2;3)\) oznacza to, że wzór funkcji \(y=|x|\) przesuwamy o 3 do góry oraz o 2 w prawo:





Zadanie 1 

Zadanie 2 

Zadanie 4