Eszkola

Wzór na wklęsłość i wypukłość wzór

Algebraicznie

Jeżeli funkcja \(f\) ma pierwszą pochodną ciągłą na przedziale \(X\), przy czym istnieje \(f''(x)>0\) dla każdego \(x\) leżącego wewnątrz \(X\), to wykres funkcji \(f\) jest wypukły na przedziale \(X\).

Jeżeli funkcja \(f\) ma pierwszą pochodną ciągłą na przedziale \(X\), przy czym istnieje \(f''(x)<0\) dla każdego \(x\) leżącego wewnątrz \(X\), to wykres funkcji \(f\) jest wklęsły na przedziale \(X\).
 

Możemy mówić o wklęsłości w przedziale lub w punkcie, jeżeli punkt jest końcem przedziału domkniętego, to mówimy o wklęsłości (wypukłości) jednostronnej. Przykład obliczania wklęsłości zaprezentowano w odrębnym artykule. Pojęcia te są ściśle związane z punktami przegięcia definicją i przykładami zamieszczonymi w innych artykułach .


Graficznie

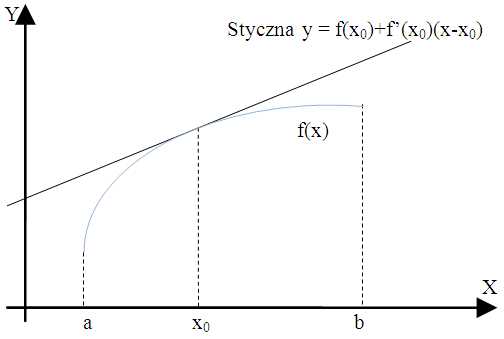
Wzór na wklęsłość i wypukłość

Krzywą o równaniu \(y=f(x)\) nazywamy wklęsłą w przedziale \((a;b)\), jeżeli krzywa ta jest położona pod styczną, poprowadzoną do krzywej w dowolnym punkcie tego przedziału.

Krzywą o równaniu \(y=f(x)\) nazywamy wypukłą w przedziale \((a;b)\), jeżeli krzywa ta jest położona nad styczną, poprowadzoną do krzywej w dowolnym punkcie tego przedziału.
 

Jak zapamiętać i zrozumieć, co to jest funkcja wypukła: wyobraźcie sobie balon, może też być piłka, który znajduje się nad wykresem w momencie, gdy jest pompowany jego ścianki się wyginają, i mają kształt jak wykresy na rysunku po lewej stronie. Analogicznie jest z funkcją wklęsła - gdybyśmy wypompowywali powietrze z piłki to ścianki jej odkształcałyby się do wewnątrz jak na rysunku po prawej (pamiętajcie, że środek piłki jest nad osią OY).
 

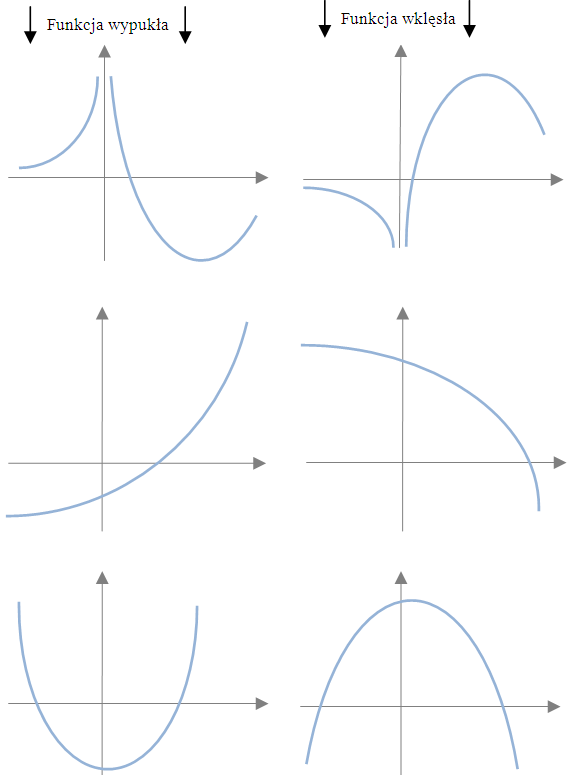
Przykłady funkcji wklęsłej i wypukłej:
Wzór na wklęsłość i wypukłość

Wzór na wklęsłość i wypukłość - jak stosować w praktyce?

8-1 =

Oprócz - wzór na wklęsłość i wypukłość może Ci się przydać

Zobacz również