Logarytmy - opis

Logarytm

Aby zrozumieć pojęcie logarytmów, należy mieć opanowane podstawy z potęgowania liczb.



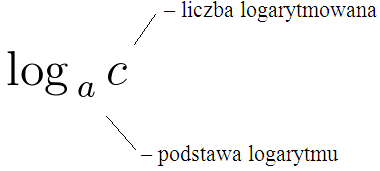
Powyższy logarytm czytamy: -logarytm o podstawie a z liczby c; lub - logarytm liczby c przy podstawie a.

Definicja logarytmu

Niech \(a>0\) i \(a\neq 1\) oraz \(c>0\). Logarytmem \(\log_{a} c\) liczby \(c\) przy podstawie \(a\) nazywamy wykładnik \(b\) potęgi, do której należy podnieść podstawę \(a\), aby otrzymać liczbę c:
 

Chcąc zrozumieć, czym jest logarytm, trzeba uświadomić sobie, że logarytm to wykładnik potęgi, czyli \(b\) we wzorze \(a ^b = c\). Aby znaleźć (obliczyć) wartość logarytmu, trzeba znaleźć odpowiedź na pytanie:

Do jakiej potęgi podnieść liczbę \(a\) aby otrzymać liczbę \(c\)? 

Przykład
\(\log_{3} 9=?\)

Do jakiej potęgi podnieść liczbę 3 aby otrzymać 9, jest to liczba 2, więc:

\(\log_{3} 9=2\)

Podstawowe własności logarytmów to:

\(\log_{a}1=0\)

\(\log_{a}a=1\)

\(\log_{a}a^b=b\)

Wynikają one z definicji. Po więcej wzorów zapraszam do zapoznania się z artykułem właściwości i wzory logarytmów.

Przykładowe zadania

Zad. 1) Oblicz wartość logarytmów:

a) \(\log_{2} 1\)

b) \(\log_{6} 1\)

c) \(\log_{12} 1\)

d) \(\log_{\sqrt{3}} 1\)

e) \(\log_{203} 1\)     Zobacz rozwiązanie

Zad. 2) Oblicz wartość logarytmów:

a) \(\log_{2} 2\)

b) \(\log_{4} 4\)

c) \(\log_{12} 12\)

d) \(\log_{\sqrt{5}} \sqrt{5}\)

e) \(\log_{903} 903\)      Zobacz rozwiązanie

Zad. 3) Oblicz wartość logarytmów:

a) \(\log_{2} 4\)

b) \(\log_{3} 9\)

c) \(\log_{2} 32\)

d) \(\log_{3} 27\)

e) \(\log_{5} 125\)      Zobacz rozwiązanie