Siłą, która działa w kierunku przeciwnym do przesunięcia ciała i proporcjonalną do wartości tego przesunięcia nazywamy siłą harmoniczną. Ruch, który wykonuje ciało pod wpływem takiej siły jest opisywany przez funkcje harmoniczne i nazywany ruchem harmonicznym.
Przykładem siły harmonicznej jest siła sprężysta \(\overrightarrow{F}\), która działa na masę \(m\) umieszczoną na sprężynie o współczynniku sprężystości \(k\), która jest wychylone z położenia równowagi o \(\overrightarrow{\Delta x}\). Wtedy:
\(\overrightarrow{F}=-k \overrightarrow{\Delta x}\)
Znak minus oznacza, że siła zawsze skierowana jest do położenia równowagi. Jeżeli pominiemy tarcie i inne opory ruchu, to zależność wychylenia od czasu \(x(t)\) masy na sprężynie wychylonej początkowo z położenia równowagi o \(A\) przyjmie postać:
\(x(t)=A\cdot cos(\omega\cdot t)\)
gdzie \(A\) jest amplitudą drgań - maksymalnym wychyleniem z położenia równowagi, a przesunięcie fazowe \(\omega=\sqrt{\dfrac{k}{m}}\)
Ogólnie, w przypadku oscylatora harmonicznego należy uwzględnić jeszcze fazę początkową \(\phi\), co prowadzi do ogólnego rozwiązania równania ruchu oscylatora harmonicznego:
\(x(t)=A\cdot cos(\omega \cdot t + \phi)\)
W momentach największego wychylenia prędkość będzie najmniejsza, a największa przy przechodzeniu przez położenie równowagi. Podobna zależność łączy funkcje sinus i kosinus - gdy jedna przyjmuje maksimum, druga ma wartość zero. Zależność prędkości od czasu \(v(t)\) będzie następująca:
\(v(t)=-A\omega \cdot sin(\omega \cdot t + \phi)\)
Przy czym \(A\cdot \omega\) można uznać za maksymalną wartość prędkości w tym ruchu. Przyspieszenie \(a(t)\) będzie zmieniać się zgodnie z zależnością:
\(a(t)=-A\omega^2\cdot cos(\omega\cdot t +\phi)\)
Maksymalne przyspieszenie będzie miało ciało, gdy siła będzie największa, czyli przy maksymalnym wychyleniu. Wyniesie ono \(a=A\cdot \omega^2\).
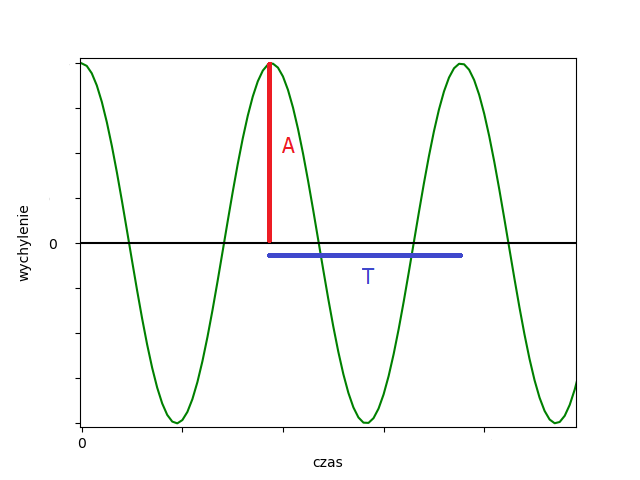
Okresem ruchu \(T\) nazywamy czas przejścia od położenia maksymalnego wychylenia do kolejnego takiego położenia. Poniższy wykres ilustruje zależność wychylenia \(x(t)\). Zaznaczono
też amplitudę na czerwono oraz okres na niebiesko. amplitudę na czerwono oraz okres na niebiesko.
Ruch harmoniczny Wasze opinie