Spadek swobodny
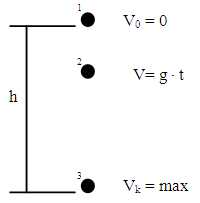
Spadek swobodny jest to fizyczne pojęcie, które w uproszczony sposób opisuje ruch ciała, które na początku znajdowało się w spoczynku i w reakcji na siłę grawitacji zaczęło się poruszać (spadać). Pamiętajcie, że w szkole średniej nie uwzględniamy oporów powietrza, dlatego z obliczeń może wam wyjść, że kamień spada tak samo jak piórko (co było by prawdą gdyby spadały w próżni). Tak więc rozpatrujemy wyłącznie oddziaływanie siły grawitacji danego obiektu np. ziemi na nasze ciało, które spada swobodnie. Uproszczeniem jest również przyjęcie stałego współczynnika grawitacji, który najczęściej opisujemy jako \(g=9,81 [\frac{m}{s^2}]\) lub nawet równego \(10\), pamiętajcie, przyspieszenie ziemskie w różnych miejscach na ziemi jest inne, najmniejsze jest na równiku a największe na biegunach (bo ziemia jest spłaszczona), ogólnie im bliżej środka ziemii tym wartość przyspieszenia ziemskiego jest większa.
Ciało w spadku swobodnym porusza się ruchem jednostajnie przyspieszonym. Możemy więc stosować wzory na przyspieszenie:
\(a=\frac{V}{t}\) oraz \(S=\frac{a\cdot t^2}{2}\)
z małą zmianą przyspieszenie \(a\) zastąpimy przyspieszeniem ziemskim \(g\), natomiast przebytą drogę \(S\) zamienimy na przebytą wysokość \(h\), w wyniku tego i po małym przekształceniu otrzymamy:
\({\color{DarkRed}{V=g\cdot t}}\) oraz \({\color{DarkRed}{h=\frac{g\cdot t^2}{2}}}\)
z małą zmianą przyspieszenie \(a\) zastąpimy przyspieszeniem ziemskim \(g\), natomiast przebytą drogę \(S\) zamienimy na przebytą wysokość \(h\), w wyniku tego i po małym przekształceniu otrzymamy:
\({\color{DarkRed}{V=g\cdot t}}\) oraz \({\color{DarkRed}{h=\frac{g\cdot t^2}{2}}}\)
gdzie:
\(V\) - prędkość ciała w danym momencie \([\frac{m}{s}]\)
\(g\) - przyspieszenie ziemskie, wynosi \(9,81\: [\frac{m}{s^2}]\), może być inne jeśli ciało było by np. na księżycu wyniosłoby \(g_k=1,622[\frac{m}{s^2}]\)
\(t\) - czas \([s]\)
\(h\) - wysokość jaką przebyło ciało \([m]\)
Jednak jeśli chcemy obliczyć na jakiej wysokości aktualnie znajduje się ciało od poziomu zero powinniśmy skorzystać z wzoru:
\({\color{DarkRed}{h=h_0-\frac{g\cdot t^2}{2}}}\)
gdzie:
\(h\) - wysokość na jakiej się znajduje ciało \([m]\)
\(h_0\) - wysokość początkowa ciała \([m]\)
\(g\) - przyspieszenie ziemskie, wynosi \(9,81\: [\frac{m}{s^2}]\), może być inne jeśli ciało było by np. na księżycu wyniosłoby \(g_k=1,622[\frac{m}{s^2}]\)
\(t\) - czas \([s]\)
Aby wyprowadzić jeszcze jeden wzór powinniśmy skorzystać z zasady zachowania energii. W naszym przypadku ciało posiada energię potencjalną i kinetyczną. jednak na samym początku zanim jeszcze zaczęło spadać posiadało zerową energie kinetyczną (bo prędkość ciała była równa zero) oraz maksymalną energię potencjalną, natomiast w momencie zetknięcia z podłożem, w najniższym punkcie lotu sytuacja się odwraca - energia kinetyczna jest maksymalna (bo prędkość ciała na dole jest największa) oraz energia potencjalna wynosi zero (bo wysokość ciała wynosi zero). W takim przypadku możemy powiedzieć, że energia kinetyczna ciała w punkcie 3 jest równa energii potencjalnej ciała w punkcie 1, czyli:
\(E_k=E_p\)
\(\frac{m\cdot V^2}{2}=m\cdot g \cdot h\)
co po przeksztąłceniu daje nam:
\({\color{DarkRed}{V=\sqrt{2\cdot g\cdot h}}}\)
Wzory zaznaczone kolorem ciemnoczerwonym, oraz ich przekształcenia dają nam wszystkie potrzebne wzory do obliczania spadku swobodnego.
Wzory:
na prędkość:
\({\color{DarkBlue}{V=g\cdot t}}\) lub \({\color{DarkBlue}{V= \sqrt{2\cdot g\cdot h}}}\)
na wysokość:
\({\color{DarkBlue}{h=\dfrac{g\cdot t^2}{2}}}\) lub \({\color{DarkBlue}{h=\dfrac{V^2}{2\cdot g}}}\) ewentualnie \({\color{DarkRed}{h_1=h_0-\frac{g\cdot t^2}{2}}}\)
na czas:
\({\color{DarkBlue}{t=\dfrac{V}{g}}}\) lub \({\color{DarkBlue}{t=\sqrt{\dfrac{2\cdot h}{g}}}}\)
gdzie:
\(V\) - prędkość ciała w danym momencie \([\frac{m}{s}]\)
\(g\) - przyspieszenie ziemskie, wynosi \(9,81\: [\frac{m}{s^2}]\), może być inne jeśli ciało było by np. na księżycu wyniosłoby \(g_k=1,622[\frac{m}{s^2}]\)
\(t\) - czas \([s]\)
\(h\) - wysokość jaką przebyło ciało \([m]\)
\(h_1\) - wysokość na jakiej się znajduje ciało \([m]\)
\(h_0\) - wysokość początkowa ciała \([m]\)
Spadek swobodny Wasze opinie