Rzut poziomy

Rzut poziomy wszystkie niezbędne wzory, wyjaśniamy wyprowadzenia wzorów i zasady ich stosowania. Omówione zjawisko rzutu poziomego. Sprawdź na naukowcu.

Co oznacza rzut poziomy?

Pojęcie rzut poziomy oznacza ruch ciała, któremu nadano prędkość początkową \(V_0\), o kierunku prostopadłym do linii sił pola grawitacyjnego. Dla zobrazowania wyobraźcie sobie, że będąc na planecie Ziemia, trzymając w ręku kamień, możecie rzucić go prosto przed siebie, wtedy tor lotu kamienia nazywamy rzutem poziomym, proszę pamiętać, że w szkole średniej jest ono traktowane z bardzo dużym uproszczeniem, ponieważ Ziemia jest okrągła i linie sił pola grawitacyjnego nie są równoległe do siebie (jak w kuli są promieniste), nie jest uwzględniany opór powietrza, a powietrze powoduje wyhamowywanie rzuconego ciała - rzucając reklamówkę czy kartkę papieru przed siebie zauważymy, że bardzo szybko się zatrzyma i spadnie - bez powietrza leciałoby dużo dalej tak jak kamień.

Zajmiemy się właśnie takim uproszczonym (jak w szkole średniej) pojęciem rzutu poziomego.



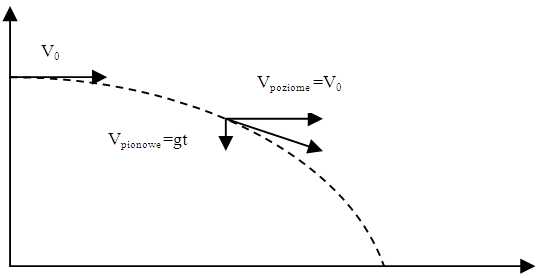
Rzut poziomy najlepiej wyobrazić sobie jako złożenie dwóch ruchów:

1) Ruchu poziomego - który jest ruchem jednostajnym
2) Ruchu pionowego - ruch jest jednostajnie przyspieszony (gdy rozpatrywać bez ruchu poziomego można nazwać - spadkiem swobodnym)

Rzut poziomy - wzory

1) O składowej poziomej wiemy, że opisana jest ruchem jednostajnym z prędkością \(V_0\), tak więc wzór ruchu na osi \(X\) możemy zapisać:

\(x= V_0\cdot t\)

gdzie:

\(x\) - odległość pozioma, jaką przebyło ciało \([m]\)

\(V_0\) - prędkość początkowa nadana ciału (skierowana poziomo) \([\dfrac{m}{s}]\)

\(t\) - czas lotu ciała \([s]\)

aby obliczyć czas lotu, potrzebny do pokonania odległości poziomej \(x\) przekształcamy wzór do postaci:

\(t= \dfrac{x}{V_0}\)

2) Składowa pionowa prędkości ciała jest opisana wzorem:

\(y=\dfrac{g\cdot t^2}{2}\)

gdzie:

\(y\) - wysokość jaką przebyło ciało \([m]\)

\(g\) - współczynnik grawitacji (\(9,81 [\dfrac{m}{s^2}]\))

\(t\) - czas lotu \([s]\)

jest to ruch jednostajnie przyspieszony o przyspieszeniu \(g\), pamiętajcie, że mowa o Ziemi - na księżycu byłoby to \(1,622 \dfrac{m}{s^2}\)), czyli im ciało dłużej spada tym szybciej się porusza.

Teraz połączymy dwa wzory, aby uzmysłowić wam, jakim torem porusza się ciało w rzucie poziomym. Do wzoru na wysokość w miejsce czasu podstawmy czas wyliczony z wzoru na poziomą składową:

\(y=\dfrac{g\cdot t^2}{2}\) oraz \(t= \dfrac{x}{V_0}\) da nam

\(y=\dfrac{g\cdot {(\frac{x}{V_0})}^2}{2}=\dfrac{g\cdot x^2}{2\cdot {(V_0)}^2}=\dfrac{g}{2\cdot {(V_0)}^2}\cdot x^2\)

jak wiemy współczynnik \(g\) oraz \(V_0\) są stałymi tak więc cały wzór ma postać:

\(y= a\cdot x^2\) dla jeśli za podstawimy za \(a=\dfrac{g}{2\cdot {(V_0)}^2}\)

widzimy więc, że ciało rzucone poziomo będzie się poruszało po torze paraboli (proszę pamiętać, że nie uwzględniamy oporów powietrza). Czasem wzory prezentowane są w inny sposób, jednak cała różnica polega na podstawieniu za \(x\) oraz \(y\) następujących symboli:

\(x=\:\:S\:\:= \:\:x(t)\)

\(y= \:\:H\:\:=\:\:h\:\:=\:\:y(t)\)


Najczęściej przy rzucie swobodnym używamy:



                  
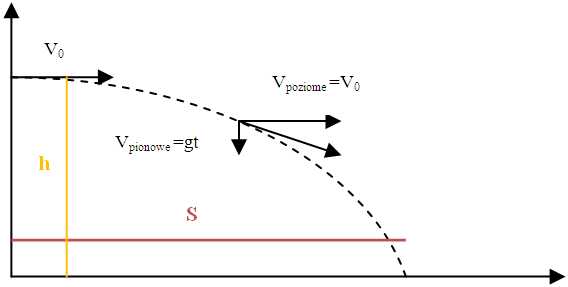
aby obliczyć odległość, na jaką rzucone zostanie ciało:

\({\color{DarkRed}{S=V_0\cdot \sqrt{\dfrac{2\cdot h}{g}}}} \)     lub     \({\color{DarkRed}{S=V_0\cdot t}}\)

aby obliczyć czas lotu ciała:

\({\color{DarkRed}{t=\sqrt{\dfrac{2\cdot h}{g}}}} \)     lub     \({\color{DarkRed}{t=S\cdot V_0}}\)

aby obliczyć wysokość, jaką przebyło ciało:

\({\color{DarkRed}{h=\dfrac{g\cdot t^2}{2}}} \)     lub     \({\color{DarkRed}{h=\dfrac{g\cdot S^2}{2\cdot v_0^2}}}\)

gdzie:

\(S\) - zasięg rzutu \([m]\)

\(V_0\) - prędkość początkowa \([\dfrac{m}{s}]\)

\(h\) - wysokość, na jakiej znajduje się ciało \([m]\)

\(g\) - przyspieszenie ziemskie \(9,81\: [\dfrac{m}{s^2}]\), ale może też być inne przyspieszenie np. księżyca, w zależności gdzie się znajdujemy

\(t\) - czas \([s]\)

Można też rozpatrywać ten przypadek jak wpisany w układ współrzędnych - ma on kształt paraboli o wzorze:



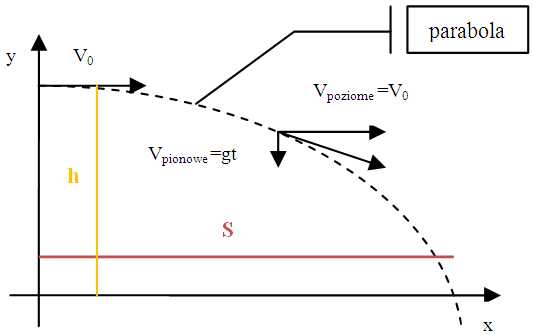
\({\color{DarkRed}{y=h-\dfrac{g}{2\cdot V_0^2}\cdot x^2}}\)

gdzie:

\(y\) - wysokość na jakiej znajduje się ciało \([m]\)

\(V_0\) - prędkość początkowa \([\dfrac{m}{s}]\)

\(h\) - wysokość początkowa (z jakiej rzucone było ciało) \([m]\)

\(g\) - przyspieszenie ziemskie \(9,81\: [\dfrac{m}{s^2}]\), ale może też być inne przyspieszenie np. księżyca, w zależności gdzie się znajdujemy

\(t\) - czas \([s]\)