Ogólnie mówiąc rzut pionowy jest to rzucenie, np. piłki pionowo w górę, najpierw piłka wznosi się a następnie spada. Na ciało działa tylko siła grawitacji. Dokładniej - rzut pionowy to pojęcie fizyczne, w którym mamy na początku nieruchome ciało, po nadaniu mu prędkości początkowej skierowanej w górę, ciało zaczyna się poruszać pionowo w górę a następnie zaczyna spadać i upada dokładnie w to samo miejsce. W szkole średniej mamy kilka uproszczeń tego pojęcia, jednym z nich jest brak uwzględniania oporów powietrza. Takim właśnie uproszczonym zjawiskiem się zajmiemy.
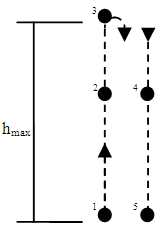
Podział rzutu pionowego na etapy lotu:
1) na początku ciało znajduje się na zerowej wysokości (na ziemi) bez ruchu
2) następnie po nadaniu prędkości początkowej ciało porusza się w górę ruchem jednostajnie opóźnionym (leci w górę ale coraz wolniej bo grawitacja na nie oddziaływuje)
3) osiąga najwyższy punkt lotu na u bardzo mały ułamek sekundy
4) następnie zaczyna spadać ruchem jednostajnie przyspieszonym (dokładnie tak jak w spadku swobodnym)
5) rozpatrywanie rzutu pionowego kończymy w momencie zetknięcia się ciała z podłożem, czyli w ułamku sekundy gdy ciało spadając zaczyna dotykać ziemi, nie rozpatrujemy czy odbije się od ziemi czy się w nią wbije a może rozbije, to nas już nie interesuje.
Proszę pamiętać, że nie uwzględniamy tu oporów powietrza, więc nie istotne jest czy wyrzucamy w górę kamień czy piórko - jedno i drugie zachowa się tak samo. Przejdźmy do opisania tego ruchu wzorami.
Ciało na początku ma nadaną prędkość \(V_0\). porusza się w górę, jednak działa na nią siła grawitacji, to znaczy na ciało działa przyspieszenie ziemskie, porusza się więc ruchem jednostajnie zmiennym (przyspieszonym, opóźnionym). Wzór dla ruchu jednostajnie przyspieszonego (lub opóźnionego - to to samo tylko czasem trzeba dodać minus w obliczeniach):
\(V=a\cdot t\)
w naszym przypadku mamy dwie zmiany, mianowicie przyspieszenie \(a\) jest przyspieszeniem ziemskim czyli \(a=g=9,81[\frac{m}{s^2}]\), oraz mamy nadaną prędkość początkową o zwrocie przeciwnym do zwrotu (kierunku działania) siły grawitacji dlatego jedno trzeba odjąć od drugiego:
\({\color{DarkRed}{V=V_0-g\cdot t}}\)
natomiast wzór na drogę w ruchu jednostajnie przyspieszonym:
\(S=\frac {a\cdot t^2}{2}\)
przekształcimy wstawiając zamiast \(S=h\) bo droga przebyta to wysokość teraz, zamiast przyspieszenia wstawimy przyspieszenie ziemskie \(a=g\) oraz dodamy prędkość początkową i otrzymamy wzór:
\({\color{DarkRed}{h=V_0\cdot t -\dfrac{g\cdot t^2}{2}}}\)
w obu wzorach założyliśmy, że kierunek dodatni jest skierowany w górę, oznacza to, że jeśli wyjdzie nam dodatni wynik prędkości to ciało się wznosi, a jeśli ujemny to oznacza, że spada, jeśli wyjdzie nam wysokość ujemna to będzie znaczyło, że ciało spadło poniżej punktu początkowego, (czyli najpierw się wzniosło i jak zaczęło spadać to minęło punkt z którego wystartowało i spadało dalej - niżej). Możemy zawsze dodać do wzoru kolejny warunek początkowy jakim jest wysokość początkowa, czyli np. wysokość podrzucanej piłki liczymy od podłogi ale samą piłkę wyrzucamy z wysokości dłoni czyli nadajemy jej wysokość początkową:
\({\color{DarkRed}{h=h_0+V_0\cdot t -\dfrac{g\cdot t^2}{2}}}\)
teraz obliczymy miejsca charakterystyczne w naszym ruchu. Zacznijmy od obliczenia czasu po jakim nasze ciało znajdzie się w najwyższym punkcie lotu, do tego posłużymy się powyższym wzorem na prędkość:
\(V=V_0-g\cdot t\)
przekształcimy go aby wyliczyć \(t\)
\(t=\frac{V_0-V}{g}\)
prędkość naszego ciała w najwyższym punkcie będzie wynosiła zero \(V=0\) po wstawieniu tego do wzoru otrzymamy:
Czas po jakim ciało osiągnie maksymalna wysokość
\({\color{DarkRed}{t=\frac{V_0}{g}}}\)
w naszym przypadku mamy dwie zmiany, mianowicie przyspieszenie \(a\) jest przyspieszeniem ziemskim czyli \(a=g=9,81[\frac{m}{s^2}]\), oraz mamy nadaną prędkość początkową o zwrocie przeciwnym do zwrotu (kierunku działania) siły grawitacji dlatego jedno trzeba odjąć od drugiego:
\({\color{DarkRed}{V=V_0-g\cdot t}}\)
natomiast wzór na drogę w ruchu jednostajnie przyspieszonym:
\(S=\frac {a\cdot t^2}{2}\)
przekształcimy wstawiając zamiast \(S=h\) bo droga przebyta to wysokość teraz, zamiast przyspieszenia wstawimy przyspieszenie ziemskie \(a=g\) oraz dodamy prędkość początkową i otrzymamy wzór:
\({\color{DarkRed}{h=V_0\cdot t -\dfrac{g\cdot t^2}{2}}}\)
w obu wzorach założyliśmy, że kierunek dodatni jest skierowany w górę, oznacza to, że jeśli wyjdzie nam dodatni wynik prędkości to ciało się wznosi, a jeśli ujemny to oznacza, że spada, jeśli wyjdzie nam wysokość ujemna to będzie znaczyło, że ciało spadło poniżej punktu początkowego, (czyli najpierw się wzniosło i jak zaczęło spadać to minęło punkt z którego wystartowało i spadało dalej - niżej). Możemy zawsze dodać do wzoru kolejny warunek początkowy jakim jest wysokość początkowa, czyli np. wysokość podrzucanej piłki liczymy od podłogi ale samą piłkę wyrzucamy z wysokości dłoni czyli nadajemy jej wysokość początkową:
\({\color{DarkRed}{h=h_0+V_0\cdot t -\dfrac{g\cdot t^2}{2}}}\)
teraz obliczymy miejsca charakterystyczne w naszym ruchu. Zacznijmy od obliczenia czasu po jakim nasze ciało znajdzie się w najwyższym punkcie lotu, do tego posłużymy się powyższym wzorem na prędkość:
\(V=V_0-g\cdot t\)
przekształcimy go aby wyliczyć \(t\)
\(t=\frac{V_0-V}{g}\)
prędkość naszego ciała w najwyższym punkcie będzie wynosiła zero \(V=0\) po wstawieniu tego do wzoru otrzymamy:
Czas po jakim ciało osiągnie maksymalna wysokość
\({\color{DarkRed}{t=\frac{V_0}{g}}}\)
wiedząc, że dokładnie symetrycznie sytuacja wygląda gdy ciało leci do góry jaki i kiedy leci w dół możemy wyciągnąć wniosek, że czas lotu do góry jest taki sam jak przy locie w dół więc:
Czas lotu ciała do momentu powrotu na to samo miejsce jest dwa razy dłuższy od czasu po jakim osiągnie maksymalną wysokość:
\({\color{DarkRed}{t=\frac{2\cdot V_0}{g}}}\)
wzór ten może być dokładniejszy uzupełniony o wysokość początkową - czas trwania lotu ciała w rzucie pionowym
aby obliczyć maksymalną wysokość na jaką wzniesie się ciało należy do wzoru na wysokość ciała podstawić czas po którym ciało osiągnie maksymalną wysokość:
do wzoru: \(h=V_0\cdot t -\dfrac{g\cdot t^2}{2}\) podstawiamy \(t=\frac{V_0}{g}\) i otrzymujemy:
\(h_{max}=V_0\cdot \frac{V_0}{g} -\dfrac{g\cdot {(\frac{V_0}{g})}^2}{2}=\frac{V_0^2}{g}-\frac{V_0^2}{2\cdot g}=\frac{V_0^2}{2\cdot g}\)
podsumowując:
Maksymalna wysokość jaką osiągnie ciało rzucone pionowo do góry wyniesie:
\({\color{DarkRed}{h_{max}=\frac{V_0^2}{2\cdot g}}}\)
wzór ten może być dokładniejszy uzupełniony o wysokość początkową - maksymalna wysokość ciała w rzucie pionowym
Wyjaśnienie symboli:
\(V\) - prędkość ciała w danym momencie \([\frac{m}{s}]\)
\(V_0\) - prędkość początkowa nadana ciału \([\frac{m}{s}]\)
\(a\) - przyspieszenie \([\frac{m}{s^2}]\)
\(g\) - przyspieszenie ziemskie \(9,81\:[\frac{m}{s^2}]\), ale może też być inne przyspieszenie dla przykładu przyspieszenie księżyca wynosi \(1,622\:[\frac{m}{s^2}]\), w zależności gdzie się znajdujemy
\(S\) - przebyta droga \([m]\)
\(h\) - wysokość na jakiej znajduje się ciało \([m]\)
\(h_{max}\) - wysokość maksymalna jaką osiągnie ciało \([m]\)
\(t\) - czas \([s]\)
\(V_0\) - prędkość początkowa nadana ciału \([\frac{m}{s}]\)
\(a\) - przyspieszenie \([\frac{m}{s^2}]\)
\(g\) - przyspieszenie ziemskie \(9,81\:[\frac{m}{s^2}]\), ale może też być inne przyspieszenie dla przykładu przyspieszenie księżyca wynosi \(1,622\:[\frac{m}{s^2}]\), w zależności gdzie się znajdujemy
\(S\) - przebyta droga \([m]\)
\(h\) - wysokość na jakiej znajduje się ciało \([m]\)
\(h_{max}\) - wysokość maksymalna jaką osiągnie ciało \([m]\)
\(t\) - czas \([s]\)
Rzut pionowy (rzut w górę) Wasze opinie