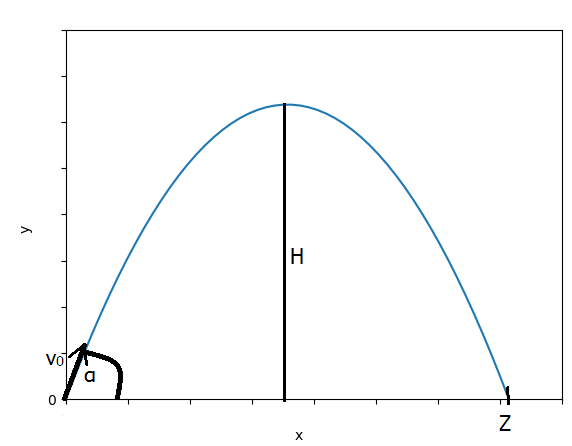
Rzutem ukośnym nazywamy ruch ciała, któremu nadano prędkość początkową pod pewnym kątem do poziomu w jednorodnym polu grawitacyjnym.
Rozważmy ciało, któremu nadano prędkość początkową \(v_0\) pod kątem \(\alpha\) do poziomu. Ruch takiego ciała można opisać jako złożenie dwóch ruchów: w kierunku poziomym i pionowym. Poziomo na ciało nie będą działały żadne siły, więc będzie poruszać się z prędkością, jaką nadano na początku. Składowa pozioma prędkości będzie równa
\(v_x=v_0 \cdot cos(\alpha)\) i będzie niezmienna w czasie.
Natomiast w kierunku pionowym ciało będzie wykonywać pod wpływem siły grawitacji ruch jednostajnie opóźniony, wznosząc się oraz jednostajnie przyspieszony, opadając z przyspieszeniem o wartości \(g \approx 9.81 \dfrac{m}{s^2}\). Prędkość wzdłuż osi pionowej \(v_y(t)\) będzie zmieniać się w czasie zgodnie z zależnością
\(v_y(t)= v_0 \cdot sin(\alpha)-g\cdot t\)
Kiedy wartość prędkości będzie dodatnia, ciało będzie się wznosić, a gdy będzie ujemna - ciało będzie opadać. Wyrażenie \(v_0 \cdot sin(\alpha)\) opisuje początkową składową prędkości w kierunku pionowym.
Położenie wzdłuż osi poziomej \(x(t)\) będzie zmienne w czasie, jak położenie w ruchu jednostajnym z prędkością \(v_x\):
\(x(t)=v_x\cdot t= v_0\cdot t\cdot sin(\alpha)\),
Wzdłuż osi pionowej położenie \(y(t)\) będzie dane wyrażeniem:
\(y(t)=v_0\cdot t\cdot sin(\alpha) - \dfrac{1}{2}g\cdot t^2\)
Ruch będzie odbywał się do momentu, kiedy ciało nie zetknie się z podłożem, czyli pionowa składowa położenie nie osiągnie zera, czyli \(y(t)=0\), co stanie się po czasie
\(t_k=\dfrac{2v_0 \cdot sin(\alpha)}{g}\).
Znając czas całego rzutu można określić zasięg rzutu \(Z\), czyli odległość, na jakiej znajdzie się ciało w momencie upadku na podłoże. Będzie to \(Z=x(t_k)=v_0\cdot cos (\alpha) \cdot \dfrac{2v_0 \cdot sin(\alpha)}{g}=\dfrac{v_0^2}{g}sin(2\alpha)\)
Na maksymalnej wysokości \(H\) ciało będzie znajdować się w połowie czasu lotu, czyli po czasie
\(t_h=\dfrac{v_o\cdot sin(\alpha)}{g}\), zatem
\(H=y(t_s)=v_0 \cdot sin(\alpha) \cdot \dfrac{v_0 \cdot sin(\alpha)}{g}-\dfrac{1}{2}g\cdot (\dfrac{v_0 \cdot sin(\alpha)}{g})^2 = \dfrac{v_0^2 \cdot sin^2(\alpha)}{2g}\)
Tor ruchu będzie określony równaniem paraboli \(y(x)= x \cdot tg(\alpha)-\dfrac{g}{2v_0^2 cos^2(\alpha)}x^2\)
Świat sportu pełen jest przykładów rzutu ukośnego. W popularnych dyscyplinach jest to kopnięcie piłki przez zawodnika podczas meczu, odbicie piłki w siatkówce czy rzut do kosza. Również wystrzał z pistoletu pod kątem można opisać jako rzut ukośny. Analogicznie zachowuje się też pojedynczy ładunek w jednorodnym polu elektrycznym. Warto zauważyć, że rzut poziomy i rzut pionowy to szczególne przypadki rzutu ukośnego.
Rzut ukośny Wasze opinie