Soczewka – najczęściej zbudowana jest ze szkła (jednak nie jest to konieczne), niezbędne jest by była przeźroczysta, najczęstszym kształtem soczewki jest wycinek walca, ale w miejscu podstaw ograniczona jest powierzchniami kulistymi (wklęsłymi lub wypukłymi), parabolicznymi lub walcowymi. Materiał, z którego zbudowana jest soczewka posiada inny współczynnik załamania światła niż ośrodek, w którym się znajduje, dokładniej chodzi o to by fala, która była przed soczewką, po wejściu w nią zmieniła swój kierunek. Rozpatrując soczewki nie mamy do czynienia tylko ze światłem, dlatego uniwersalnie powinno się używać pojęcia załamanie fali a nie światła, ponieważ występują też soczewki akustyczne, które mają załamywać fale dźwiękowe. W szkole mówiąc o soczewkach mówi się o szklanej strukturze, jednak mogą być one zbudowane zarówno z ciał stałych, jak i ciekłych czy gazowych.
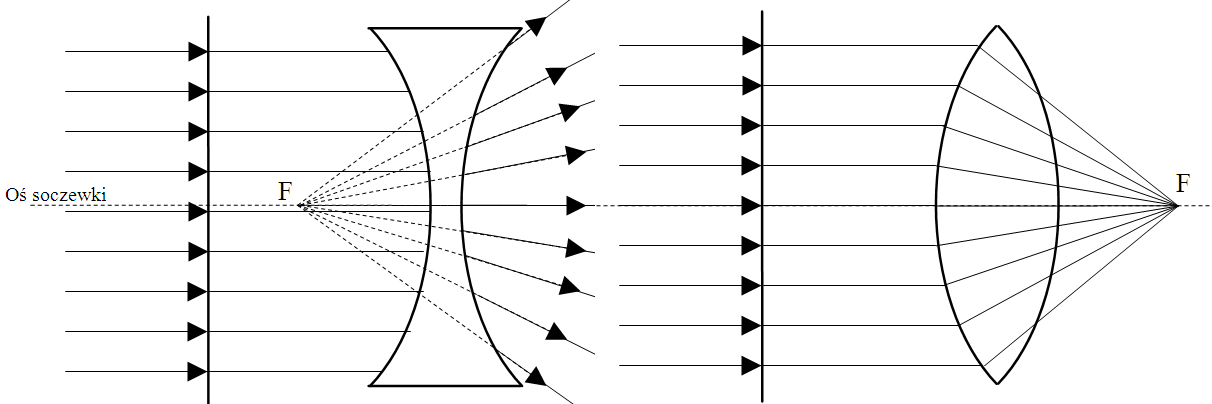
Podstawowym podziałem soczewek jest ich zdolność skupiająca, wyróżniamy soczewki skupiające (na rysunku po prawej) oraz soczewki rozpraszające (na rysunku po lewej).
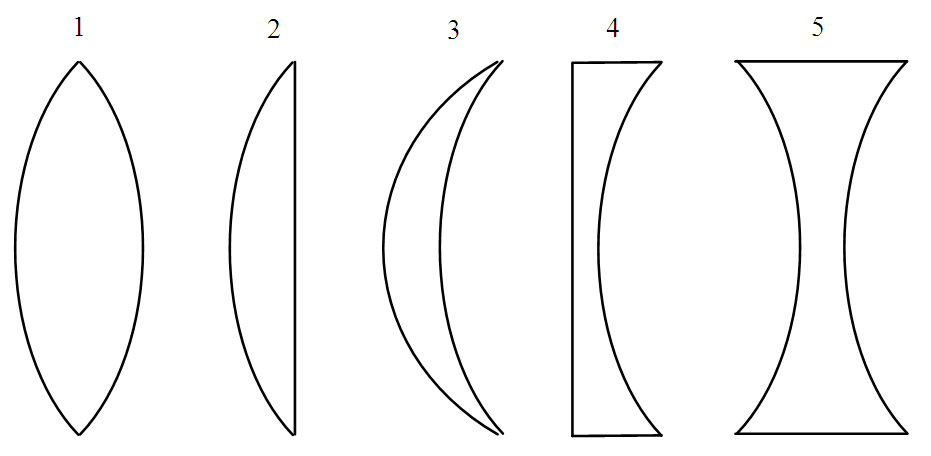
Soczewki można podzielić w zależności od konstrukcji na soczewki pojedyncze (jak szkło w okularach) i złożone (jak soczewka Fresnela wykorzystywana w latarniach morskich). Najbardziej rozpowszechnionym podziałem soczewek jest ich podział ze względu na kształt i tu można wyróżnić soczewki:
1) dwuwypukłe
2) płasko-wypukła
3) wklęsło-wypukła
4) płasko-wklęsla
5) dwuwklęsła
Każda soczewka posiada oś optyczną i punkt zwany ogniskową. Soczewki są ograniczone przez powierzchnie kuliste będące wycinkami kul, środki tych kul wyznaczają prostą która jest osią optyczną soczewki. Ogniskowa soczewki jest punktem oznaczanym literą F, który leży na osi optycznej soczewki, w tym punkcie przecinają się kierunki fal lub ich przedłużenia.
Do opisu matematycznego soczewki cienkiej stosuje się wzór:
\(\dfrac{1}{f}=\dfrac{1}{x}+\dfrac{1}{y}=\left ( \dfrac{n_2}{n_1}-1 \right )\left ( \dfrac{1}{r_1}+\dfrac{1}{r_2} \right )\)
z uwzględnieniem, że kąt między promieniami fal a osią soczewki jest niewielki oraz:
\(f\) – odległość ogniskowej od soczewki
\(n_1\) – współczynnik załamania ośrodka, w którym znajduje soczewka
\(n_2\) – współczynnik załamania soczewki
\(r_1\), \(r_2\) – promienie powierzchni kulistych soczewki
\(x\) – odległość przedmiotu od soczewki
\(y\) – odległość obrazu od soczewki
Dla promieni \(r\) powierzchni kulistych przyjmuje się znak dodatni dla powierzchni wypukłych, a ujemny dla powierzchni wklęsłych, dla płaskich przyjmuje się \(r=\infty\) co dla \(\dfrac{1}{r}=\dfrac{1}{\infty}=0\) daje zero. Odległość ogniskowej \(f\) od soczewki jest dodatnia dla soczewek skupiających oraz ujemna dla soczewek rozpraszających.
Należy pamiętać, że opis matematyczny przedstawia soczewkę cienką która w uproszczony sposób odwzorowuje rzeczywistość.
Soczewka Wasze opinie
bardzo dokładny opis