W zależności od podłączenia rezystorów do obwodu ich całkowita rezystancja może mieć różną wartość nawet jeśli zostaną użyte te same oporniki.
Rozważmy połączenie trzech oporników, tak, że przewód wychodzący z jednego opornika bezpośrednio podłączony jest do drugiego. Połączenie takie nazywane jest szeregowym. Rezystory tworzą w nim umowny szereg, co ilustruje poniższa grafika:
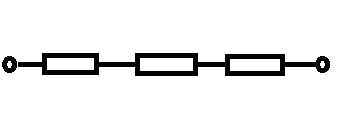
Zaznaczono na niej symbolem prostokąta trzy oporniki we fragmencie obwodu elektrycznego. Zakładając, że każdy z nich ma opór \(R\), to opór zastępczy tego fragmentu obwodu wynosi: \(R_z=R+R+R=3R\).
Ogólnie dla \(n\) oporników o oporach \(R_1,R_2,...,R_n\) połączonych szeregowo, opór zastępczy jest sumą oporów: \(R_z=R_1+R_2+...R_n\)
Inną możliwością podłączenia jest konstrukcja, w której oporniki nie są połączone bezpośrednio ze sobą, tylko znajdują się na gałęziach o tej samej różnicy potencjałów. Połączenie takie nazywane jest równoległym. Obrazuje to poniższa grafika:
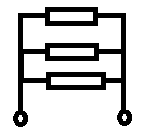
Zakładając, że każdy opornik ma opór \(R\), to opór zastępczy tego fragmentu obwodu wynosi:
\(R_z=\frac{R}{3}\)
Ogólnie dla \(n\) oporników o oporach \(R_1,R_2,...,R_n\) połączonych równolegle, opór zastępczy jest odwrotnością sumy odwrotności oporów: \(R_z=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_n}}\)
Łączenie oporników Wasze opinie