Ruch po okręgu

Ruch po okręgu to ruch, którego torem jest okrąg. Jeżeli na punkt materialny będzie działała siła prostopadła do prędkości, to będzie ona powodować zakrzywienie toru ruchu. Siła ta nazywana jest siłą dośrodkową. Ze względu na to, że jest ona prostopadła do prędkości, to stale będzie zakrzywiać tor ruchu i będzie źródłem przyspieszenia dośrodkowego. W wyniku działania siły dośrodkowej ciało może wykonywać ruch po okręgu.

Wzór na ruch po okręgu

W ruchu po okręgu promień wodzący punktu w czasie \(t\) zakreśla kąt \(\Theta\). Można na tej podstawie określić średnią prędkość kątową na tym łuku \(\omega\)
 \(\omega=\dfrac{\Theta}{t}\)
Kąt \(\Theta\) zwykle wyrażany jest w radianach, stąd jednostką prędkości kątowej jest radian na sekundę.

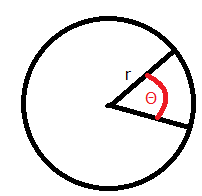
Okresem  \(T\) w ruchu po okręgu nazywany jest czas wykonania obrotu promienia wodzącego \(\overrightarrow{r}\) o kąt pełny. W ciągu okresu punkt materialny pokonuje drogę \(l\) równą długości okręgu. Gdy promień okręgu wynosi \(r\) jest to \(l=2\pi \cdot r\), w związku z tym prędkość liniowa \(v\) w ruchu po okręgu wynosi
\(v=\dfrac{l}{T}=\dfrac{2\pi \cdot r}{T}\)

Prędkość liniowa jest styczna do toru ruchu w każdym jego punkcie.

Ponieważ w mierze radialnej \(2\pi\) jest miarą kąta pełnego (który jest zakreślany w czasie \(t=T\)) można wskazać zależność łączącą prędkość kątową i liniową

\(v=\omega \cdot r\)

Miarą zmiany prędkości kątowej jest przyspieszenie kątowe \(\epsilon\). Wyraża ono szybkość zmiany prędkości kątowej w czasie i określane jest formułą
 \(\epsilon = \dfrac{\Delta \omega}{\Delta t}\)
gdzie \(\Delta \omega\) jest zmianą prędkości kątowej w czasie \(\Delta t\)

Jednostką przyspieszenia kątowego jest \([\epsilon]=\dfrac{rad}{s^2}\)

W przypadku ruchu po okręgu można mówić też o częstotliwości \(f\), która opisuje, jak często zostaje wykonany jeden pełny obieg i można ją wyznaczyć ze wzoru \(f=\dfrac{1}{T}\)
Jednostką częstotliwości jest Hz (herc).

Ruch po okręgu - przykład

Przykładem ruchu po okręgu jest ruch końcówki wskazówki zegara, która w czasie \(t=24 h=86400s\) zakreśla kąt pełny, stąd jej prędkość kątowa wynosi \(\omega=\dfrac{2\pi}{86400} \dfrac{rad}{s}\). Za ruch po okręgu można traktować też ruch satelity geostacjonarnego – siłą dośrodkową jest w tym przypadku siła grawitacji, a okres ruchu takiego satelity wynosi niecałe 24 godziny, dzięki czemu  zachowuje on stałą pozycję nad wybranym punktem równika.