Geometria analityczna - związana jest z umieszczonymi w kartezjańskim układzie współrzędnych figur geometrycznych, odcinków i prostych. Geometria analityczna umożliwia nam wyliczenie:
- długości odcinka \(\overrightarrow{AB}\)
znając współrzędne początku tego wektora A = (x1, x2) oraz końca B = (y1, y2)
\(|AB|= {\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} }\)
Przykład 1. Wyznacz długość odcinka o współrzędnych A = (1, -5) oraz B = (2, 3)
\(|AB|= {\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} }\)
\(|AB|= {\sqrt{(2-1)^2+(3-(-5))^2} } = {\sqrt{1^2+8^2} }= {\sqrt{1+64} }= {\sqrt{65} }\)
Odcinek \(\overrightarrow{AB}\) ma długość \({\sqrt{65} }\)
- Środek odcinka \(\overrightarrow{AB}\) znając współrzędne początku tego wektora A = (x1, x2) oraz końca B = (y1, y2)
\(S =( {x_1+x_2 \over 2}+ {y_1+y_2 \over 2})\)
Przykład 2. Wyznacz środek odcinka o współrzędnych A = (1, -5) oraz B = (2, 3)
\(S =( {x_1+x_2 \over 2}+ {y_1+y_2 \over 2})\)
\(S =( {1+2 \over 2}, {-5+3 \over 2})=({3 \over 2},{-2 \over 2})=(1{1 \over 2},-1)\)
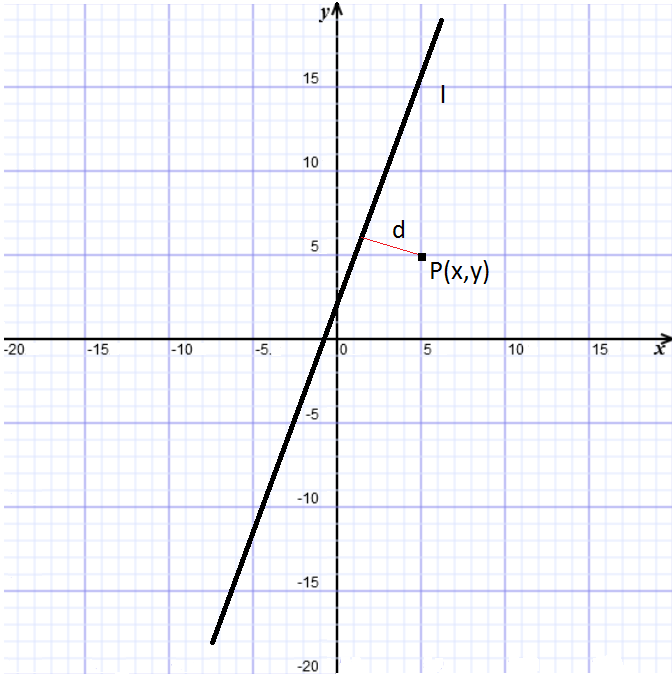
- odległość punktu P (x,y) od prostej l wyrażonej w postaci ogólnej prostej tzn: Ax + By + C = 0
\(d = {|Ax+By+C| \over {\sqrt{A^2+B^2} }}\)
Przykład 3. Oblicz odległość punktu A = (3, 4) od prostej y = 2x + 3
przekształcam równanie prostej do postaci ogólnej Ax + By + C = 0 i otrzymuję 2x - y + 3 = 0 i podstawiam do wzoru
\(d = {|Ax+By+C| \over {\sqrt{A^2+B^2} }}\)
\(d = {|2*3-1*4+3| \over {\sqrt{2^2+(-1)^2} }}={|6-4+3| \over {\sqrt{4+2} }}={|5| \over {\sqrt{5} }}={5 \over {\sqrt{5} }}\)
Geometria analityczna Wasze opinie