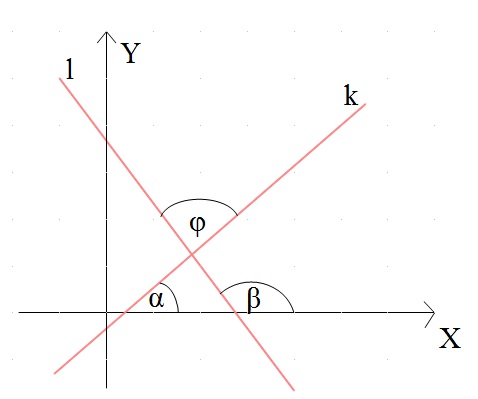
Z rysunku wynika: \(\alpha + \varphi = \beta\), czyli \(\varphi = \beta - \alpha\)
\(tg \varphi = tg(\beta - \alpha) = \left |\dfrac{tg \beta - tg \alpha}{1+ tg \beta \: tg \alpha}\right | = \left |\dfrac{a_1 - a_2}{1 + a_1 \cdot a_2}\right |\)
Czyli aby wyliczyć kąt między dwiema prostymi należy wstawić współczynniki kierunkowe do wzoru:
\(tg \varphi = \dfrac{a_1 - a_2}{1 + a_1 \cdot a_2}\)
a nastepnie odczytać wartość kąta lub obliczyć za pomocą funkcji \(arctg( \dfrac{a_1 - a_2}{1 + a_1 \cdot a_2})\) dla wyliczonej wartości funkcji.
Wyjaśnienie symboli:
\(\varphi\) - kąt między dwiema prostymi
\(a_1, a_2\) - współczynniki kierunkowe prostych
\(b_1, b_2\) - wyrazy wolne prostych
\(arctg()\) - funkcja arkustangens (odwrotność tangensa)
Kąt między dwiema prostymi Wasze opinie