Płaszczyzna - to płaska część rozciągająca się w nieskończoność
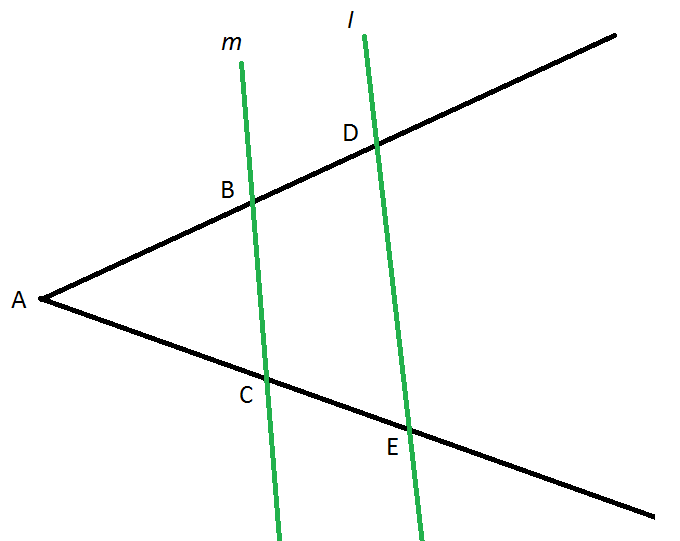
Twierdzenie Talesa - jeżeli ramiona dowolnego kąta przetniemy dwoma równoległymi prostymi m II l to prawdziwe są następujące zależności:
\({AB \ \over AC}={BD \ \over CE}\)
\({AB \ \over AD}={AC \ \over AE}\)
\({BC\ \over AB}={DE \ \over AD}\)
\({AC \ \over AE}={BC \ \over DE}\)
Wzajemne położenie prostej i okręgu - Jeżeli przyjmiemy, że punkt d (P, k) to jest odległość punktu P od prostej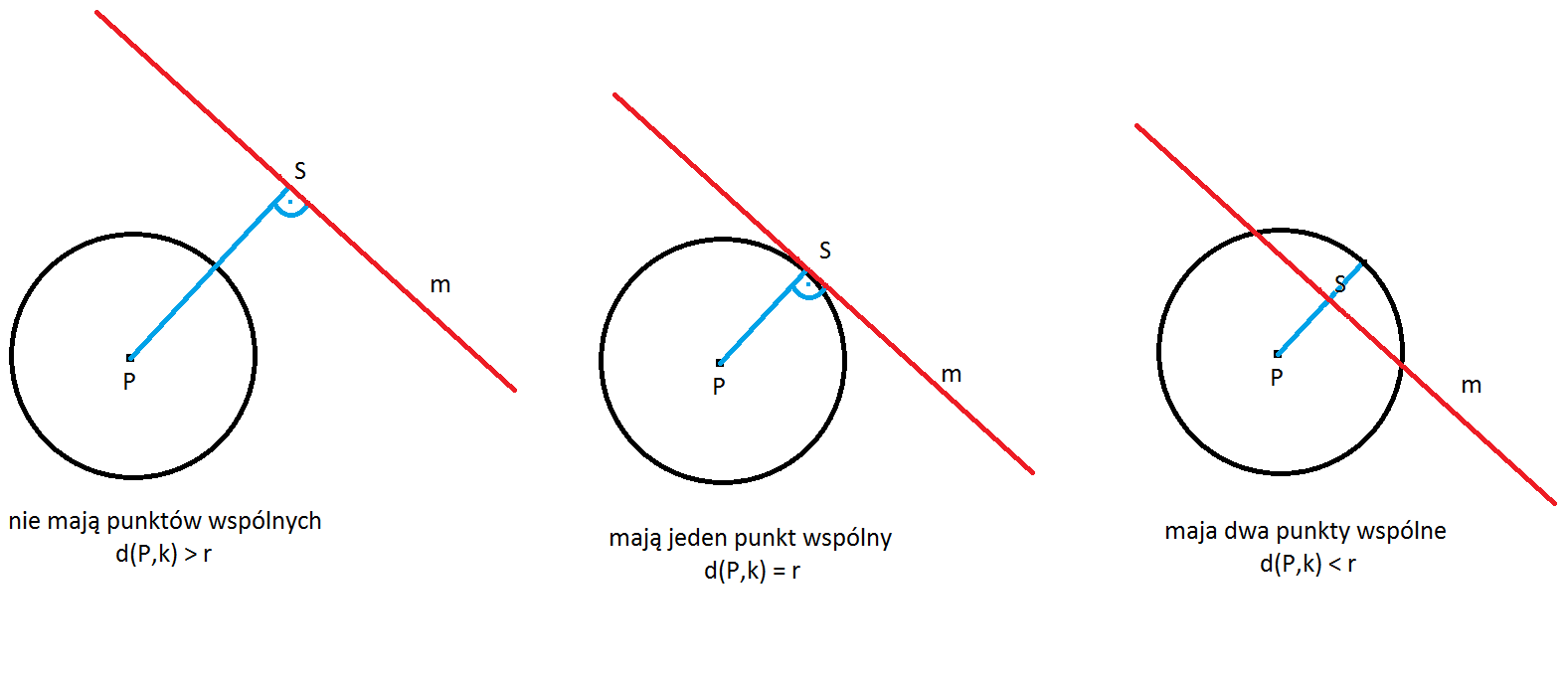
Twierdzenie Talesa Wasze opinie