Jeżeli ramiona kąta przetniemy dwoma prostymi równoległymi to długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu.
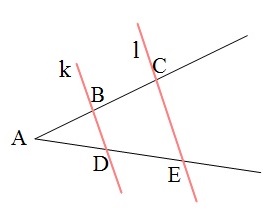

Jeśli \(k || l\) , to:
\(\dfrac{|AB|}{|AD|} = \dfrac{|BC|}{|DE|}\)
\(\dfrac{|AB|}{|BC|} = \dfrac{|AD|}{|DE|}\)
\(\dfrac{|AB|}{|AC|} = \dfrac{|AD|}{|AE|}\)
\(\dfrac{|AB|}{|AC|} = \dfrac{|AD|}{|DE|} = \dfrac{|BD|}{|CE|}\)
Twierdzenie Talesa - jak stosować w praktyce?