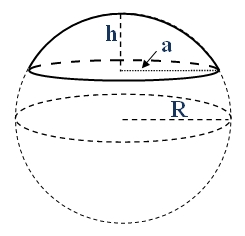
Wzór na pole powierzchni czaszy kulistej ma postać:
\(P = P_b + P_p\)
\(P_b = 2 \pi R h\)
\(P_p = \pi a^2\)
\(P = 2 \pi R h +\pi a^2\)
\(a = \sqrt{R^2 - (R - h)^2}\)
Wyjaśnienie symboli:
\(P\) - pole powierzchni całkowitej czaszy kulistej
\(P_b\) - pole powierzchni wycinka kuli
\(P_p\) - pole podstawy wycinka kuli
\(h\) - wysokość czaszy
\(R\) - promień kuli
Wzór na pole powierzchni czaszy kulistej
Przydatne kalkulatory i narzędzia
Może Ci się przydać:
Zobacz również
- Pole powierzchni warstwy kulistej
- Przekątna prostopadłościanu
- Potęga pierwiastka o tym samym...
- Zamiana funkcji arc sin na inne
- Suma i różnica funkcji...
- Dzielenie pierwiastków
- Pole powierzchni torusa
- Wzór na odległość punktu od prostej
- Reguła de l'Hospitala
- Całkowanie przez części
- Objętość czaszy kulistej
- n-ty wyraz ciągu arytmetycznego
- Wzór Newtona
- Objętość stożka ściętego
- Objętość wycinka kuli