
Równanie prostej \(l\) przechodzączej przez dwa różne punkty na płaszczyźnie \(A(x_1, y_1)\) oraz \(B(x_2, y_2)\) ma postać:
\(l: y - y_1 = \dfrac{y_2 - y_1}{x_2 -x_1} (x - x_1)\), gdy
\(x_1 \neq x_2\)
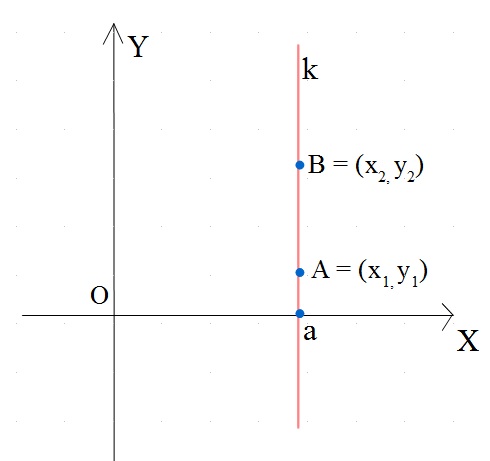
Równanie prostej \(k\) przechodzączej przez dwa różne punkty na płaszczyźnie \(A(x_1, y_1)\), \(B(x_2, y_2)\) leżące na prostej równoległej do osi \(OY\) ma postać:
\(k: x = a\), gdy
\(x_1 = x_2 = a\)
Wzór na równanie prostej przechodzącej przez dwa punkty - jak stosować w praktyce?