 Wzór na objętość beczki, gdy tworzącą jest łuk paraboli ma postać:
Wzór na objętość beczki, gdy tworzącą jest łuk paraboli ma postać:\(V = \dfrac{\pi h}{15}(8 R^2 + 4 r R + 3r^2)\)
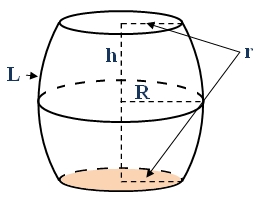
Wyjaśnienie symboli:
\(V\) - objętość beczki
\(h\) - wysokość beczki
\(R\) - promień beczki w najszerzyszm punkcie
\(r\) - promień beczki w najwęższym punkcie
Wzór na objętość beczki, gdy tworzącą jest łuk koła ma postać:
\(V \approx \pi h \dfrac{1}{3}(2 R^2 + r^2)\)
Wyjaśnienie symboli:
\(V\) - objętość beczki
\(h\) - wysokość beczki
\(R\) - promień beczki w najszerzyszm punkcie
\(r\) - promień beczki w najwęższym punkcie
Wzór na objętość beczki - jak stosować w praktyce?