Pierwsze prawo Kirchhoffa traktuje o natężeniach w węźle: suma natężeń prądów wpływających jest równa sumie natężeń prądów wypływających z węzła. Więcej informacji znajdziesz się poniżej.
Pierwsze prawo Kirchhoffa - wzór
Jeżeli przez \(I_{in}\) oznaczymy sumę natężeń prądów wpływających, a przez \(I_{out}\) prądów wypływających, to:
\(I_{in}=I_{out}\)
Dla przykładu w poniższym obwodzie do węzła wpływają prądy o natężeniach \(I_2\) oraz \(I_4\), a wypływają \(I_1\) oraz \(I_3\)
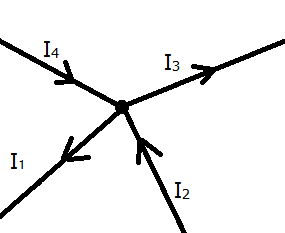
Można zatem zapisać:
\(I_2+I_4=I_1+I_3\)
lub w równoważnej postaci, jeżeli prądy wypływające uwzględni się ze znakiem minus: \(-I_1+I_2-I_3+I_4=0\)
Drugie prawo Kirchhoffa
Drugie prawo Kirchhoffa traktuje o spadkach napięcia w oczku: suma spadków napięć w oczku jest równa sumie sił elektromotorycznych.
Lub w równoważnej postaci: suma przyrostów i spadków napięć w oczku jest równa zero.
Korzystając z tego prawa należy określić kierunek przechodzenia oczka (strzałka wewnątrz), jeżeli siły SEM działają w tym kierunku należy uwzględnić je ze znakiem plus, jeżeli w przeciwnym, ze znakiem minus. Napięcia na opornikach należy uwzględnić ze znakiem minus, gdy kierunek przepływu prądu jest zgodny z kierunkiem przechodzenia oczka, a ze znakiem plus, jeżeli jest przeciwny.
Dla przykładu w obwodzie poniżej ustalono kierunek przechodzenia oczka zgodny z ruchem wskazówek zegara. Siła elektromotoryczna \(\epsilon_1\) oraz \(\epsilon_2\) działają zgodnie z tym kierunkiem, będą zatem uwzględnione ze znakiem plus. Przez oporniki prąd przepływa zgodnie z kierunkiem przechodzenia, więc spadki napięć będą uwzględnione ze znakiem minus. Ostatecznie:
\(\epsilon_1 + \epsilon_2 - IR_1 - IR_2=0\)
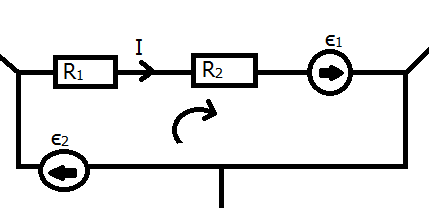
Oporniki są tutaj połączone szeregowo, więc natężenie prądu przepływającego jest takie samo, wynosi \(I\), a napięcie na opornikach \(U_1=I\cdot R_1\)oraz \(U_2=I\cdot R_2\)zgodnie z prawem Ohma.
Prawa Kirchhoffa Wasze opinie
Super prawo! Polecam każdemu