\(P = 2 \pi b(b + \dfrac{a}{\epsilon} arc \: sin \: \varepsilon)\)
gdzie \(a > b\)
\(\varepsilon = \sqrt{1 - \frac{b^2}{a^2}}\)
Wyjaśnienie symboli:
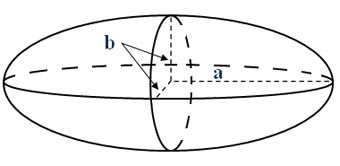
\(P\) - pole powierzchni elipsoidy obrotowej wydłużonej
\(a\), \(b\) - półosie elipsoidy obrotowej wydłużonej
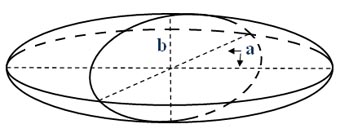
Wzór na pole powierzchni elipsoidy obrotowej spłaszczonej ma postać:
\(P = 2 \pi a^2 + \dfrac{\pi b^2}{\varepsilon} ln \dfrac{1 + \varepsilon}{1 - \varepsilon}\)
gdzie \(a > b\)
\(\varepsilon = \sqrt{1 - \frac{b^2}{a^2}}\)
Wyjaśnienie symboli:
\(P\) - pole powierzchni elipsoidy obrotowej spłaszczonej
\(a\), \(b\) - półosie elipsoidy obrotowej spłaszczonej
Wzory na pola powierzchni elipsoidy obrotowej - jak stosować w praktyce?