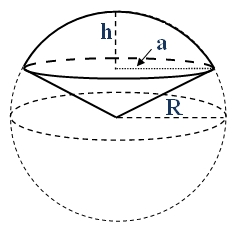
Wzór na pole powierzchni wycinka kuli ma postać:
\(P = \pi R (2h + a)\)
\(a = \sqrt{R^2 - (R - h)^2} = \sqrt{h(2R - h)}\)
Wyjaśnienie symboli:
\(P\) - pole powierzchni wycinka kuli
\(R\) - promień kuli
\(h\) - wysokość czaszy
Wzór na pole powierzchni wycinka kuli wzór
Przydatne kalkulatory i narzędzia
Oprócz - wzór na pole powierzchni wycinka kuli może Ci się przydać
Zobacz również
- Twierdzenie Bézouta - wzór
- Pole powierzchni części wspólnej...
- n-ty wyraz ciągu geometrycznego - wzór
- Funkcja okresowa - wzór
- Objętość warstwy kulistej - wzór
- Wariacja z powtórzeniami - wzór
- Pole powierzchni koła - wzór
- Objętość ostrosłupa prawidłowego - wzór
- Wyznacznik macierzy 4x4 - wzór
- Parzystość i nieparzystość funkcji -...
- Łączność mnożenia - wzór
- Macierz odwrotną 4x4 - wzór
- Objętość wycinka kuli - wzór
- Logarytm pierwiastka - wzór
- Logarytm iloczynu - wzór
Wzór na pole powierzchni wycinka kuli - jak stosować w praktyce?