Energia mechaniczna jest sumą energii kinetycznych ciał tworzących układ fizyczny i energii potencjalnych wszystkich oddziałujących ze sobą ciał tego układu:
\(E_{mechaniczna}=E_k+E_p\)
Energia kinetyczna ciała (lub układu ciał) jest zależna od masy i prędkości według wzoru:
\(E_k=\frac{mv^2}{2}\) , gdzie:
m - masa ciała
v - prędkość z jaką ciało się porusza
Ciało będące w ruchu posiada energię kinetyczną. W tym samym czasie ciało może posiadać również energię potencjalną, jeśli znajduje się na pewnej wysokości względem danego poziomu odniesienia np. jabłko spadające z drzewa na powierzchnię ziemi.
Energię potencjalną ciała wyrażamy za pomocą wzoru:
\(E_p=mgh\) , gdzie:
m - masa ciała
g - przyspieszenie ziemskie
h - wysokość
Zgodnie z zasadą zachowania energii mechanicznej w dowolnym ruchu przebiegającym bez tarcia (i innych strat energii) energia mechaniczna układu izolowanego jest stała (\(E{mechaniczna}=const\))..
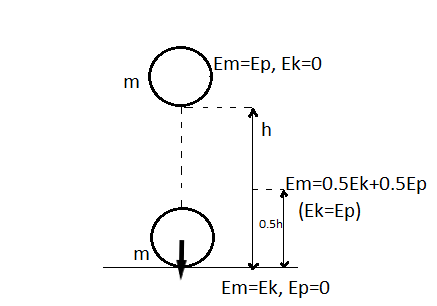
Przeanalizujmy spadek swobodny ciała o masie m na skutek działania siły grawitacji. Początkowo ciało znajduje się na wysokości h i jego prędkość wynosi zero. Posiada ono więc energie mechaniczną równą: \(E_{mechaniczna}=E_p=mgh\) . W momencie upuszczenia ciała zaczyna się ono poruszać ruchem jednostajnie przyspieszonym z przyspieszeniem ziemskim \(g=9,81[\frac{m}{s^2}]\). W pewnym punkcie (w połowie drogi) energia kinetyczna jest równa energii potencjalnej. Suma energii kinetycznej i potencjalnej pozostaje stała. Gdy ciało zderza się z ziemią uzyskuje prędkość maksymalną, wysokość względem powierzchni ziemi jest równa zero, dlatego \(E_p=0\) ,energia kinetyczna przyjmuje wtedy wartość maksymalną równą energii mechanicznej: \(E_{mechaniczna}=E_k=\frac{mv^2}{2}\).
W każdym momencie zdarzenia suma energii kinetycznej i potencjalnej jest stała i równa energii mechanicznej:
\(E_{mechaniczna}= E_k+E_p=const\)
Energia mechaniczna i jej przemiany Wasze opinie