Rozwiąż nierówność, wyniki przedstaw na osi liczbowej
a) \( \frac{x}{3}+\frac{x+1}{3}>1\)
b) \( \frac{x+3}{2}+\frac{2x+1}{4}>\frac{3}{8}\)
c) \( \frac{5-x}{6}+\frac{1-x}{4}\leqslant \frac{1}{3}\)
d) \( x+\frac{x}{2}+\frac{x+5}{4}\leqslant \frac{x-2}{2}\)
Rozwiązanie
a)
\( \frac{x}{3}+\frac{x+1}{3}>1\)
Na początku pozbędziemy się ułamków, mnożąc przez wspólny mianownik ułamków w przykładzie, czyli 3.
\(\frac{x}{3}+\frac{x+1}{3}>1 \:\: / \: \cdot 3\)
\(3\cdot \frac{x}{3}+3\cdot \frac{x+1}{3}>3\cdot 1\)
\(x+(x+1)>3\)
\(x+x+1>3\)
\(x+x>3-1\)
\(2x>2 \:\: / \: :2\)
\(x>1\)
Nanosimy na oś liczbową:

Odpowiedź: Rozwiązaniem nierówności jest \(x \: \epsilon \: (1;+\infty)\).
b)
\( \frac{x+3}{2}+\frac{2x+1}{4}>\frac{3}{8}\)
Zaczynamy od pozbycia się ułamków, przez pomnożenie całej nierówności przez 8.
\(\frac{x+3}{2}+\frac{2x+1}{4}>\frac{3}{8} \:\: / \: \cdot 8\)
\(8\cdot \frac{x+3}{2}+8\cdot \frac{2x+1}{4}>8\cdot \frac{3}{8}\)
\(4(x+3)+2(2x+1)>3\)
\(4x+12+4x+2>3\)
\(4x+4x>3-12-2\)
\(8x>-11 \:\: / \: :8\)
\(x>-\frac{11}{8}\)
\(x>-1\frac{3}{8}\)
Nanosimy na oś liczbową:

Odpowiedź: Rozwiązaniem nierówności jest \(x \: \epsilon \: \left ( -1\frac{3}{8};+\infty \right )\).
c)
\( \frac{5-x}{6}+\frac{1-x}{4}\leqslant \frac{1}{3}\)
Pozbywamy się ułamków, mnożąc przez liczbę będącą wspólnym mianownikiem ułamków i rozwiązujemy.
\(\frac{5-x}{6}+\frac{1-x}{4}\leqslant \frac{1}{3} \:\: / \cdot 12\)
\(12\cdot \frac{5-x}{6}+12\cdot \frac{1-x}{4}\leqslant 12\cdot \frac{1}{3}\)
\(2(5-x)+3(1-x)\leqslant 4\)
\(10-2x+3-3x\leqslant 4\)
\(-2x-3x\leqslant 4-10-3\)
\(-5x\leqslant -9 \:\: / :(-5)\)
\(x\geqslant \frac{9}{5}\)
\(x\geqslant 1\frac{4}{5}\)
Nanosimy na oś liczbową:

Odpowiedź: Rozwiązaniem nierówności jest \( x \: \epsilon \: \left \langle 1\frac{4}{5};+\infty \right ) \).
d)
\( x+\frac{x}{2}+\frac{x+5}{4}\leqslant \frac{x-2}{2}\)
Pozbywamy się ułamków, przez pomnożenie całej nierówności przez 4.
\(x+\frac{x}{2}+\frac{x+5}{4}\leqslant \frac{x-2}{2} \:\: / \: \cdot 4\)
\(4\cdot x+4\cdot \frac{x}{2}+4\cdot \frac{x+5}{4} \leqslant 4\cdot \frac{x-2}{2} \)
\(4x+2x+(x+5) \leqslant 2(x-2)\)
\(4x+2x+x+5 \leqslant 2x-4\)
\(4x+2x+x-2x \leqslant -4-5\)
\(5x \leqslant -9 \:\: / \: :5\)
\(x\leqslant -\frac{9}{5}\)
\(x\leqslant -1\frac{4}{5}\)
Nanosimy na oś liczbową:
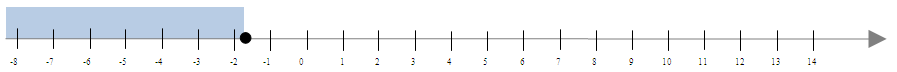
Odpowiedź: Rozwiązaniem nierówności jest \( x \: \epsilon \: \left ( -\infty;-1\frac{4}{5} \right \rangle \).
a) \( \frac{x}{3}+\frac{x+1}{3}>1\)
b) \( \frac{x+3}{2}+\frac{2x+1}{4}>\frac{3}{8}\)
c) \( \frac{5-x}{6}+\frac{1-x}{4}\leqslant \frac{1}{3}\)
d) \( x+\frac{x}{2}+\frac{x+5}{4}\leqslant \frac{x-2}{2}\)
Rozwiązanie
a)
\( \frac{x}{3}+\frac{x+1}{3}>1\)
Na początku pozbędziemy się ułamków, mnożąc przez wspólny mianownik ułamków w przykładzie, czyli 3.
\(\frac{x}{3}+\frac{x+1}{3}>1 \:\: / \: \cdot 3\)
\(3\cdot \frac{x}{3}+3\cdot \frac{x+1}{3}>3\cdot 1\)
\(x+(x+1)>3\)
\(x+x+1>3\)
\(x+x>3-1\)
\(2x>2 \:\: / \: :2\)
\(x>1\)
Nanosimy na oś liczbową:

Odpowiedź: Rozwiązaniem nierówności jest \(x \: \epsilon \: (1;+\infty)\).
b)
\( \frac{x+3}{2}+\frac{2x+1}{4}>\frac{3}{8}\)
Zaczynamy od pozbycia się ułamków, przez pomnożenie całej nierówności przez 8.
\(\frac{x+3}{2}+\frac{2x+1}{4}>\frac{3}{8} \:\: / \: \cdot 8\)
\(8\cdot \frac{x+3}{2}+8\cdot \frac{2x+1}{4}>8\cdot \frac{3}{8}\)
\(4(x+3)+2(2x+1)>3\)
\(4x+12+4x+2>3\)
\(4x+4x>3-12-2\)
\(8x>-11 \:\: / \: :8\)
\(x>-\frac{11}{8}\)
\(x>-1\frac{3}{8}\)
Nanosimy na oś liczbową:

Odpowiedź: Rozwiązaniem nierówności jest \(x \: \epsilon \: \left ( -1\frac{3}{8};+\infty \right )\).
c)
\( \frac{5-x}{6}+\frac{1-x}{4}\leqslant \frac{1}{3}\)
Pozbywamy się ułamków, mnożąc przez liczbę będącą wspólnym mianownikiem ułamków i rozwiązujemy.
\(\frac{5-x}{6}+\frac{1-x}{4}\leqslant \frac{1}{3} \:\: / \cdot 12\)
\(12\cdot \frac{5-x}{6}+12\cdot \frac{1-x}{4}\leqslant 12\cdot \frac{1}{3}\)
\(2(5-x)+3(1-x)\leqslant 4\)
\(10-2x+3-3x\leqslant 4\)
\(-2x-3x\leqslant 4-10-3\)
\(-5x\leqslant -9 \:\: / :(-5)\)
\(x\geqslant \frac{9}{5}\)
\(x\geqslant 1\frac{4}{5}\)
Nanosimy na oś liczbową:
Odpowiedź: Rozwiązaniem nierówności jest \( x \: \epsilon \: \left \langle 1\frac{4}{5};+\infty \right ) \).
d)
\( x+\frac{x}{2}+\frac{x+5}{4}\leqslant \frac{x-2}{2}\)
Pozbywamy się ułamków, przez pomnożenie całej nierówności przez 4.
\(x+\frac{x}{2}+\frac{x+5}{4}\leqslant \frac{x-2}{2} \:\: / \: \cdot 4\)
\(4\cdot x+4\cdot \frac{x}{2}+4\cdot \frac{x+5}{4} \leqslant 4\cdot \frac{x-2}{2} \)
\(4x+2x+(x+5) \leqslant 2(x-2)\)
\(4x+2x+x+5 \leqslant 2x-4\)
\(4x+2x+x-2x \leqslant -4-5\)
\(5x \leqslant -9 \:\: / \: :5\)
\(x\leqslant -\frac{9}{5}\)
\(x\leqslant -1\frac{4}{5}\)
Nanosimy na oś liczbową:
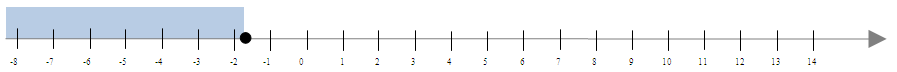
Odpowiedź: Rozwiązaniem nierówności jest \( x \: \epsilon \: \left ( -\infty;-1\frac{4}{5} \right \rangle \).
Jak obliczyć nierówności liniowe – zadanie 3 - wyniki