Ekstrapolacja równania regresji na inne dane - opis

Ekstrapolacja otrzymanej zależności pomiędzy zmiennymi w analizie regresji jest bardzo ryzykowną czynnością. Pisząc ekstrapolacja mamy tutaj na myśli "przenoszenie" uzyskanych wyników (równania regresji, zależności) na wyniki inne niż te, na których model regresji został obliczony. Jeżeli nasz model został opracowany dla pewnego zakresu to na innym zakresie danych (spoza pierwotnego) nie powinno się stosować tego samego modelu regresji.

 

Zobaczmy przykład analizy, gdzie ekstrapolacja modelu na inny zakres doprowadza do błędnych wniosków. 

Trener-badacz wykrył zależność pomiędzy liczbą godzin treningu tygodniowo a szybkością sportowca. Postawił zatem wniosek, że im sportowcy trenują więcej tym mają lepsze wyniki w teście szybkości (są szybsi). Na podstawie badania opracował równanie regresji (wzór), dzięki któremu mógł określić przyrost szybkości przy zwiększeniu danej liczby godzin treningu. Po przeprowadzonych badaniach, przed ważnymi zawodami (chcąc jak najlepiej przygotować drużynę do zawodów) zalecił zwiększenie godzin treningu dla swoich sportowców. Jednakże zwiększył on liczbę godzin treningu ponad zakres, na którym przeprowadził badanie i obliczył równanie regresji. Okazało się, że sportowcy osiągnęli gorsze rezultaty w szybkości niż wynikało to z przyjętego modelu regresji.

Opisaną sytuację zaprezentowano na wykresie poniżej.



 

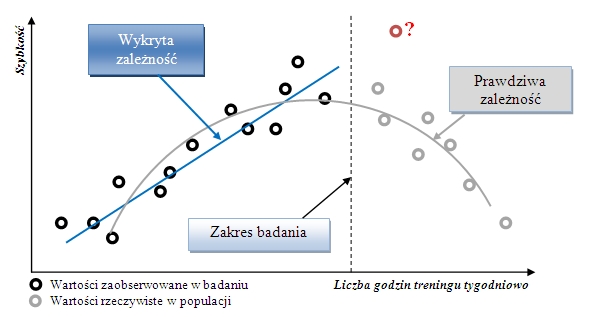
Jak można zauważyć, ekstrapolowanie uzyskanych w analizie wyników na inny zakres zmiennej wyjaśniającej (predyktora, w przykładzie: liczba godzin treningu) doprowadziła do odmiennych rezultatów niż zakładał to trener-badacz, co w rezultacie doprowadziło do tego, że drużyna gorzej wypadła w zawodach. W rzeczywistości sportowcy byli zbyt zmęczeni dodatkowymi treningami, aby móc uzyskać dobre rezultaty. Prawdziwa zależność pomiędzy liczbą godzin treningu tygodniowo a szybkością ma inną naturę dla całego zakresu analizowanych wyników niż wykrył to badacz na "ograniczonym" zakresie.
 

Badacz w pierwotnym badaniu wykrył zależność jedynie dla danego zakresu danych. Przyjął, że wykryta zależność dotyczy całego zakresu badanego zjawiska od 0 do n godzin treningu tygodniowo. W rzeczywistości zależność pomiędzy intensywnością treningu a efektami ma zależność kwadratową. Przyjęty model, zależność liniowa jest prawidłowa, ale do pewnego momentu (linia przerywana). Od tego momentu następuje spadek efektywności treningu, czego badacz nie uwzględnił w swoim badaniu, ponieważ nie wprowadził do modelu większego zakresu danych.

 

Niebezpieczeństwo ekstrapolacji dotyczy sytuacji, gdzie z różnych względów nie przeprowadziliśmy badań na innym zakresie danych a próbujemy na nie przełożyć otrzymaną zależność. Pomimo, iż wykrywamy pewien charakter zależności, np. liniowy, na szerszym zakresie może on okazać się być np. kwadratowy. Niebezpieczeństwo to najlepiej widoczne jest w ekonomii. Opracowane modele ekonomiczne są dobre dla zbadanych sytuacji, dla danego otoczenia markoekonomicznego i politycznego. Jednakże, gdy one się zmieniają to istnieje wielkie niebezpieczeństwo, że założone modele nie będą funkcjonować prawidłowo, ponieważ przy ich konstrukcji nie uwzględniano takich sytuacji, wydarzeń (nie było takich sytuacji w historii).

Wykryta zależność pomiędzy zjawiskami powinna być stosowana jedynie dla zakresu danych wejściowych, na którym została ona stworzona, ponieważ nieznana jest natura relacji pomiędzy zmiennymi w obszarze niezbadanym wcześniej.